Scheduling

参考
2-CUDA-Introduction-2-of-2
Cuda 编程之 Tiling

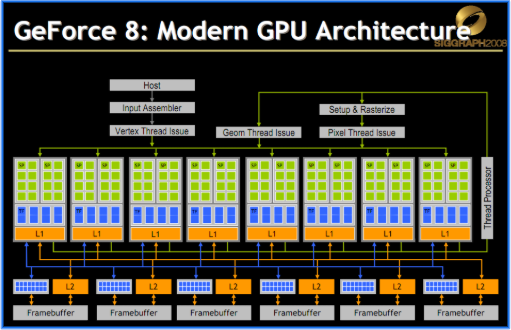
Physical Architecture

NVIDIA GeForce 8800 GTX G80-300-A2

最小的单位， SP(Streaming Processor)，然后是SPs(Streaming Processors）

以 Tesla 架构的 GeForce 8 系列搭载 G80 的 8800 GTX 为例，其拥有 16 个 Streaming Multiprocessor

Config Name	Num
Shading Units	128
TMUs	32
ROPs	24
SM Count	16
L2 Cache	96KB

相比较之下，Ada LoveLace 架构的 4070 Super 其拥有56个Streaming Multiprocessor

需要注意的是，每个SM所能含有的最大threads 是随着架构的提升而增大的，不过至今的数代都保持在了2048这个数字。

Warp

Users don’t control warp, it is hardware group of 32 consecutive “lanes”(32 threads of a block)

This is why we keep threads-per-block size as multiple of 32

• Each thread occupies 1 lane, warp lanes are consecutive threadIdx values

• Unit of sheduling and execution

• CUDA GPUs schedule warps for execution, not threads

• All threads in a warp execute same instruction at the same clock-time

• Zero-overhead context switching - All resources reside on the same SM until execution

• A block will always on the same SM

• All threads in a warp execute the same insturction

  • While all threads in a grid run the same kernel code, only threads within the same warp are guaranteed to execute the same instruction at the same time.
  • They are all working from the same set of instructions, but they are not synchronized. They run independently and can be at completely different points in the program at any time.

• Swapping sheduled warps has zero overheads

• Scheduler always tries to optimize execution

• More resources required - less warp

  • Registers: A large but limited set of super-fast memory for each thread’s private variables.

  • Shared Memory: A fixed amount of fast on-chip memory allocated to thread blocks

• One SM can handle multiple block at the same time

  • Warp Size is the unit of execution.
  • Concurrent Threads is the unit of residency. This is the total number of threads that are loaded, active, and have their resources allocated on the SM, ready to be executed.

Scenario	Registers per Thread	Max Concurrent Threads on SM	Max Concurrent Warps on SM
High Usage	64	32,768 / 64 = 512	512 / 32 = 16
Low Usage	16	32,768 / 16 = 2048	2048 / 32 = 64

Example Ⅰ

32 threads per wap but 8 SPs per SM, What gives?

When an SM shedule its

A kernal has

• 1 global memory read
• 4 non-dependent multiples/adds

How many warps are required to hide the memory latency ?

Each warp has 4 multiples/adds
16 cycles

We need to cover 200 cycles

• 200/16 = 12.5
• ceil(12.5) = 13

13 warps are required

Example Ⅱ

• What actually happens when you launch a kernel say with 100 blocks each with 64 threads?
  • Let’s say on a GT80 (i.e. 16 SMs, 8 SPs each)
  • Max T/block is 512, Max T/SM is 768 threads
  • Chip level scheduling:
    • 100 blocks of 64 threads
    • 768/64 => max 12 blocks can be scheduled for every SM
  • SM level scheduling:
    • 12 blocks = 768 threads = 24 warps
    • Warp scheduler kicks in:
      • 8 threads -> 8 threads -> 8 threads -> 8 threads（因为这个是8 SPs each）

上述描绘了无需考虑thread所使用的resources的简化情况， 注意，每个SM这里的确可以支持12个blocks，但是100个并不是说就使用9个SM，Since your 100 blocks are fewer than the GPU’s capacity of 192, the scheduler will load all 100 blocks onto the 16 SMs immediately. Some SMs will get 6 blocks, and some will get 7, until all 100 are distributed.

Divergence

What happens if branches in a warp diverge ?

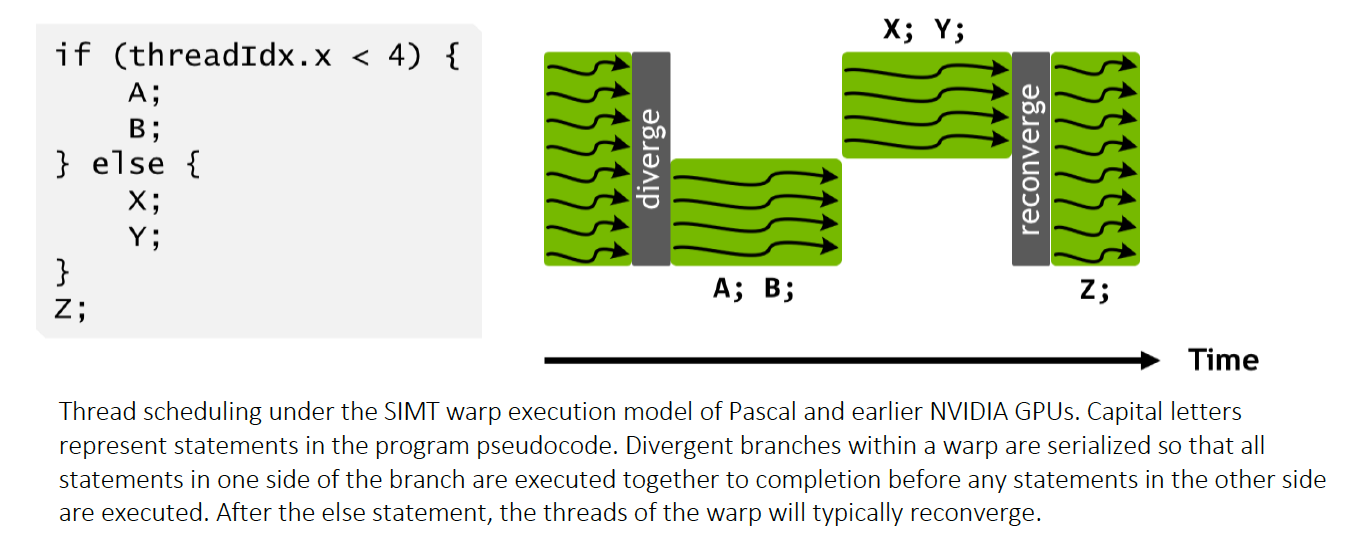
If threads within a warp take different paths in an if-else statement, the hardware has to serialize the paths, executing one after the other, which can reduce performance.

Synchronization

• Call __syncthreads();, it is on a block level

Why it is important that execution time be similar among threads ?
Long-running threads lead to inefficient stalls

Why does it only synchronize within a block?
Execution across blocks is not concurrent or ordered

Golden Role

For a __syncthreads() to work, every single thread in a block must be able to reach the same __syncthreads() call. If even one thread takes a path that skips the synchronization point, the other threads in the block will wait for it forever.

Deadlock

__global__ void faulty_kernel(float* data) {
    int idx = threadIdx.x;

    // Even and odd threads take different paths
    if (idx % 2 == 0) {
        // Even threads do some work...
        data[idx] = 1.0f;
        
        // ...and then wait here forever for the odd threads.
        __syncthreads();
    } else {
        // Odd threads are paused while the 'if' block executes.
        // They will never reach the __syncthreads() call above.
        data[idx] = 2.0f;
    }
}

1. A warp encounters an if-else statement. Some threads evaluate the condition as true, and others evaluate it as false.
2. The hardware picks one path to execute first (e.g., the if block). The threads that chose this path become active, while the threads that need to take the else path are temporarily paused (“masked off”).
3. The active threads enter the if block and hit the __syncthreads(). They now stop and wait for all other threads in their block to also arrive at this exact synchronization point.
4. Deadlock: The paused threads can never reach the __syncthreads() inside the if block because they are waiting to execute the else block. The active threads will never proceed because they are waiting for the paused threads. The entire block is now stuck in a permanent standoff.

Each __syncthreads is unique

Revisit of Matrix Multiply

The previous code:

__global__ void MatrixMultiplyKernel(const float* devM, const float* devN,
                                     float* devP, const int width)
{
int tx = threadIdx.x;
int ty = threadIdx.y;

// Initialize accumulator to 0
float pValue = 0;

// Multiply and add
for (int k = 0; k < width; k++) {
float m = devM[ty * width + k];
float n = devN[k * width + tx];
pValue += m * n;
}

// Write value to device memory - each thread has unique index to write to
devP[ty * width + tx] = pValue;
}

原来的想法很朴素，我最终的矩阵多大，我就开多少个线程去算，一个线程对应最终矩阵C的一个值。

那么这个线程去算的时候呢，要看一下矩阵A的一行，再看矩阵B的一列。最终进行乘法、相加运算。C中的每个元素的线程都要去看A和看B，那么就会带来大量的对于Global Memory的访问，这会十分低效。

直觉上打一个不恰当的比方，我们给一个大房间铺地砖的时候，应该是拿个小推车去从大货车上装个一批，然后在房间中从这个小推车上拿了地砖去铺，小推车拿空了小推车再去装一批。而不是每铺一个地砖都要去大货车中拿一块地砖。

我们要做的是，找的一种办法提升shared memory的使用，减少Global Memory的访问，这种办法可以记录某些中间状态，让矩阵C的每个元素计算不至于总是去查A和、B


图片出自Cuda 编程之 Tiling

Say, we have matrix $A$

$$
\left[ \begin{array}{cc}
2 & 6 & 7 &5 \
3 & 1 & 4 &6 \
8 & 9 & 0 &1 \
2 & 7 & 7 &4
\end{array}
\right]
$$

matrix $B$

$$
\left[ \begin{array}{cc}
1 & 6 & 2 &1 \
3 & 9 & 8 &4 \
5 & 6 & 3 &9 \
1 & 0 & 7 &2
\end{array}
\right]
$$

__global__ void MatrixMultiplyKernel(const float* devM, const float* devN,
                                     float* devP, const int width)
{
    __shared__ float sM[TILE_WIDTH][TILE_WIDTH];
    __shared__ float sN[TILE_WIDTH][TILE_WIDTH];

    int bx = blockIdx.x; 		int by = blockIdx.y;
    int tx = threadIdx.x;		int ty = threadIdx.y;

    int col = bx * width + tx;
    int row = by * width + ty;

    // Initialize accumulator to 0
    float pValue = 0;

    // Multiply and add
    for (int m = 0; m < width / TILE_WIDTH; m++) {
        sM[ty][tx] = devM[row * width + (m * TILE_WIDTH + tx)];
        sN[ty][tx] = devN[col + (m * TILE_WIDTH + ty) * Width];
        __syncthreads();

        for (int k = 0; k < TILE_WIDTH; ++k)
            pValue += sM[ty][k] * sN[k][tx];
        __syncthreads();
    }
    devP[row * width + col] = pValue;
}

for the first iteration, we have

Phase 1: Processing the First Pair of Tiles

Load Tiles into Shared Memory

matrix $sM$

$$
\left[ \begin{array}{cc}
2 & 6 \
3 & 1\
\end{array}
\right]
$$

matrix $sN$

$$
\left[ \begin{array}{cc}
1 & 6 \
3 & 9\
\end{array}
\right]
$$

__syncthreads();

Compute from Shared Memory

Our target thread (0,0) now calculates its part of the dot product using the values in the fast shared memory.

pValue += sM[0][0] * sN[0][0] + sM[0][1] * sN[1][0]
pValue += (2 * 1) + (6 * 3)
pValue = 20

Our target thread (0,1):

pValue += sM[0][0] * sN[0][1] + sM[0][1] * sN[1][1]
pValue += (2 * 6) + (6 * 9)
pValue = 66

Our target thread (1,0):

pValue += sM[1][0] * sN[0][0] + sM[1][1] * sN[1][0]
pValue += (3 * 1) + (1 * 3)
pValue = 6

Our target thread(1,1):

pValue += sM[1][0] * sN[0][1] + sM[1][1] * sN[1][1]
pValue += (3 * 6) + (1 * 9)
pValue = 27

__syncthreads();

all four of those calculations are done at the same time, in parallel.

Phase 2: Processing the Second Pair of Tiles

Load Tiles into Shared Memory

matrix $sM$

$$
\left[ \begin{array}{cc}
7 & 5 \
4 & 6\
\end{array}
\right]
$$

matrix $sN$

$$
\left[ \begin{array}{cc}
5 & 6 \
1 & 0\
\end{array}
\right]
$$

__syncthreads();

Compute from Shared Memory

Our target thread (0,0) now calculates its part of the dot product using the values in the fast shared memory.

pValue += sM[0][0] * sN[0][0] + sM[0][1] * sN[1][0]
pValue += (7 * 5) + (5 * 1)
pValue += 40

pValue = 60

Our target thread (0,1):

pValue += sM[0][0] * sN[0][1] + sM[0][1] * sN[1][1]
pValue += (7 * 6) + (5 * 0)
pValue += 42

pValue = 108

Our target thread (1,0):

pValue += sM[1][0] * sN[0][0] + sM[1][1] * sN[1][0]
pValue += (4 * 5) + (6 * 1)
pValue += 26

pValue = 32

Our target thread(1,1):

pValue += sM[1][0] * sN[0][1] + sM[1][1] * sN[1][1]
pValue += (4 * 6) + (6 * 0)
pValue += 24

pValue = 51

__syncthreads();

all four of those calculations are done at the same time, in parallel.

Now, we have the left top block of C:

$$
\left[ \begin{array}{cc}
60 & 108 \
32 & 51\
\end{array}
\right]
$$

为什么我们可以这么做？

Dot product can be done as partial nums

在naive中，我们想求一个C的元素，我们一次性去拿A的对应横行和B的对应纵行进行计算。在tiling中，我们把这个计算分为多步，对于每个我们关注的C的子矩阵，即一个block，比如例子这里就是left top block of C，我们去看原矩阵A、B对应的block，而后进行运算。这会让我们不再每求一个C的元素都要将A的对应横行和B的对应纵行全部访问一遍，而是，我关注的这个C的block在原A矩阵中的对应（横向）block 以及原B矩阵中的对应（竖向）的block块A,B,C, 做累加操作。每次我都会先缓存以下当前关注的A、B中的block，称作sM、sN
以下是block同步开始的
top left block of C

top second left block of C