Parallel Algorithm

参考
3-Parallel-Algorithms.pptx

Parallel Reduction

Arithmetic intensity: compute to memory access ratio 进行一次内存访问时，可以执行多少次计算操作。这个比值越大，往往意味着性能更好。

找到数组的和，最大值，连续积，均值

Reduction:  An operation that computes a single result from a set of data

在并行计算中，为了高效地对大量数据进行规约操作（如求和、求最大值等），算法通常采用迭代的形式。在每一轮迭代中，活动的线程会将两两配对的元素进行运算，从而将数据规模减半（因为每次迭代数据都会减半，往往是$\log_2{n}$次迭代）

数组的和

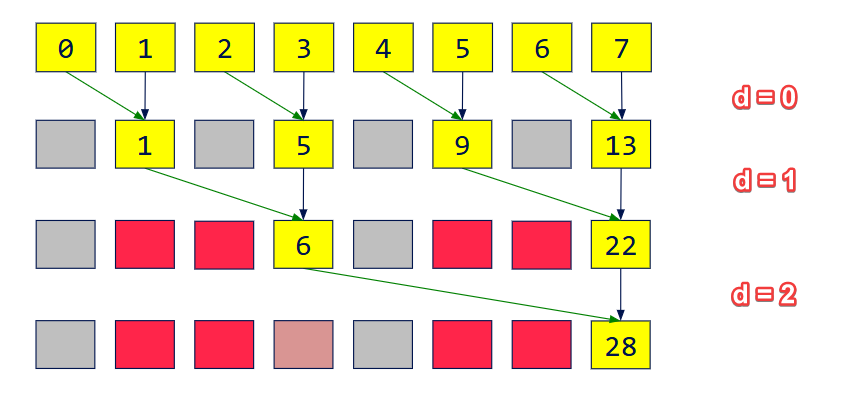
分治分冶，两个两个地求和下去
$O(logn)$ for n elements

第一行的$\log_2{n} -1$ 指的是总共的迭代次数 - 1，第一行的for是用来遍历迭代的，di表示是低几次迭代

第二行的all意味着并行，k是线程的索引， 步长为$2^{d+1}$，与迭代次数有关。例如， 若若当前迭代为第0次，那么步长为$2$，如果是第1次迭代，步长为$4$，如果是第2次迭代，步长为$8$

第三行执行了加法的具体内容。

当第0次迭代时（d=0）

for all k = 0 to n -1 by 2 in parallel
	x[k + 1] += x[k]

即，
线程0，执行x[0 + 1] += x[0]，也就是 x[1] += x[0]

线程2，执行x[2 + 1] += x[2]，也就是 x[3] += x[2]

线程4，执行x[4 + 1] += x[4]，也就是 x[5] += x[4]

以此类推…

当第1次迭代时（d=1）

for all k = 0 to n -1 by 4 in parallel
	x[k + 3] += x[k + 1]

即，
线程0，执行x[0 + 3] += x[0 + 1]，也就是 x[3] += x[1]

线程4，执行x[4 + 3] += x[4 + 1]，也就是x[7] += x[5]

Scan

All-Prefix-Sums 前缀和（前缀规约）

这里的⊕指的是二元运算，其需要两个操作数，且满足结合律运算，即(a⊕b)⊕c=a⊕(b⊕c)

$I$ 代表身份元，它是指与任何元素进行二元运算后，结果仍然是该元素的特殊值。

• 对于加法 (+)，身份元是 0，因为 a+0=a
• 对于乘法 (×)，身份元是 1，因为 a×1=a
• 对于最大值 (max)，身份元是 −∞ (负无穷大)，因为 max(a,−∞)=a

结合律对设计并行算法至关重要，因为它允许我们以任何顺序对数据进行分组和处理，而不会影响最终结果。

• Exclusive Scan
  不包括当前指向的数组中的元素
  In: [ 3 1 7 0 4 1 6 3]
  Out: [ 0 3 4 11 11 15 16 22]
• Inclusive Scan(Prescan) 闭扫描
  包括当前指向的数组中的元素
  In: [ 3 1 7 0 4 1 6 3]
  Out: [ 3 4 11 11 15 16 22 25]

如何从一个闭扫描创建开扫描（逆向扫描）？

Input: [ 3 4 11 11 15 16 22 25]
将每一位右移，在首位补Identity（对于这里是0），有
[ 0 3 4 11 11 15 16 22]
Exclusive: [ 0 3 4 11 11 15 16 22]

如何从一个开扫描创建闭扫描（逆向扫描） Prescan？

我们既需要开扫描，也需要原始的输入

$$
Inclusive[i]=Exclusive[i]+Input[i]
$$

将开扫描与原始输入的元素逐个相加，
得到最终结果 [ 3, 4, 11, 11, 15, 16, 22, 25]

A parallel algorithm for Inclusive Scan

对于单线程来说，这个算法很简单。首位照抄原始输入的首位，之后的元素从前一个元素加上原始输入当前的元素即可。

out[0] = in[0]; // assuming n > 0
for (int k = 1; k < n; ++k)
  out[k] = out[k – 1] + in[k];

若如此做，对于n个元素的数组，我们需要执行 n-1 次加法操作。

并行算法的时间复杂度是$O(logn)$，因为其不再必须等待上一步。
一般的并行化算法（Hillis-Steele）可以将工作总量变为$O(nlogn)$ ，而更高效的算法可以将工作总量优化到 $O(n)$

Native Parallel Scan

for d = 0 to (log₂n) - 1
	for all k in parallel
		if(k >= 2^(d)){
			x[k] = x[k - 2^d] + x[k];
		}

这里的d是指当前处理的是第几次迭代
注意，这里的k步长总是1， 但是其会经过$k >= 2^{d}$ 这个判断来去除一些不需要进行的运算。

由于我们无法控制线程的先后执行顺序，且算法中会出现依靠数组中其他值的情况，例如计算 Array[1] = Array[1] + Array[0]，数组中的元素可能因为被其他值更改而污染。所以在实现中使用乒乓缓存。即，在一个迭代中，只从一个数组中读，只写入另一个数组，然后交换这两个数组。

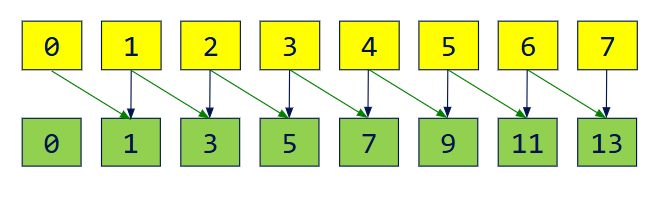
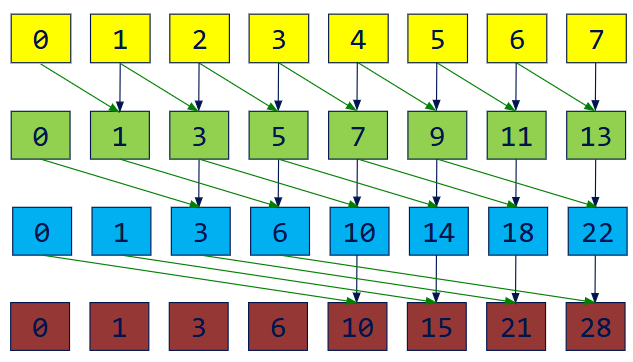
Work-Efficient Parallel Scan

若如此做，将会首先得到一个开扫描，最后进行一次逆向扫描，得到闭扫描

二叉树

利用一棵平衡二叉树来分两阶段执行Scan

假设输入是[0 1 2 3 4 5 6 7]

• Up-Sweep

// Same code as our Parallel Reduction
// 注意，这里的to是一个闭区间，包含log_2{n} - 1
for d = 0 to log_2{n} - 1
  for all k = 0 to n – 1 by 2^(d+1) in parallel
    x[k + 2^(d+1) – 1] += x[k + 2^(d) – 1];

% 是取模运算，a % b 的结果是 a 除以 b 后的余数。 6 % 2 = 0

需要指出的是，由于步长的存在，这里伪代码的k是一个稀疏的、跳跃式增长的变量，用来标记每个计算单元的起始位置，是从“外部调度者”的视角来看待的。而CUDA中的k，或者线程id是每个线程自己的视角，那么经过了((k + 1) % fullStride != 0) 这样的判断之后，线程id已经成为了实际写入数据的位置。

也就是说，在kernel函数中，对于每个线程而言，

__global__ void kernParallelScan(int paddedN, int n, int d, int* idata) {
    int k = blockIdx.x * blockDim.x + threadIdx.x;

	int halfStride = 1 << (d);
    int fullStride = halfStride * 2;

    if (k >= n || ((k + 1) % fullStride != 0)) {
        return;
    }

    // up-sweep
    idata[k] += idata[k - halfStride];
}

1. Imagine array as a tree
   Array stores only left child
   Right child is the element itself
2. For node at index n
   Left child index = n/2 (rounds down)
   Right child index = n
   

我们把这个树扫（推）上去，得到了上扫完成后的一个中间状态[0 1 2 6 4 9 6 28]

• Down-Sweep
  “下扫”的核心思想是：从树的根节点开始，将每个节点所代表的“前缀和”分配给它的子节点，直到最底层的叶子节点（也就是我们的目标数组）

1. 树顶的值换成0
2. 从上至下地，一层层地，父节点把自己的值传给左孩子，把“自己的值 + 左孩子的原始值”传给右孩子

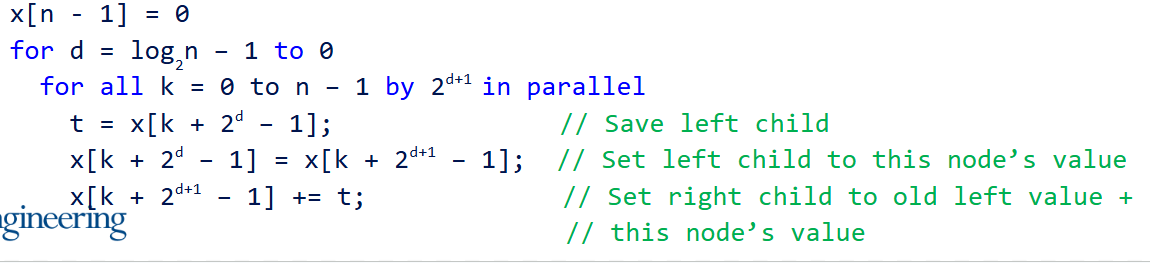
在得到我们上扫的结果后：

我们执行下列步骤：

1. 根节点的值被设置为了0（注意，这一步应该只执行一次，而不是并行时，每个线程都这样设置一下，因为对于非第一个执行的线程，其根节点已经被第一个执行的线程更新过了）

2. 蓝色层的6，拷贝父节点的值，新值变为了0；蓝色层的22，拷贝父节点的值，加上左边兄弟的原值6，新值变为6。 也就是蓝色这一层变为了[6, 22]

3. 绿色这一层进行运算。
   绿色1，拷贝父节点的值，新值为0， 绿色5，拷贝父节点的值，加上左兄弟原值，变为1

绿色9，拷贝父节点的值6，新值为6，绿色13，拷贝父节点 6，再加上左边兄弟（绿色9）的原始值 9。新值为 6 + 9 = 15。
它们的值变成了 [0, 1, 6, 15]

5. 黄色这一层进行运算，有新的黄色层[0 0 1 3 6 10 15 21]，即开扫描

6. 将开扫描加上原始输入，有闭扫描

• Up-Sweep
  $O(n)$ adds
• Down-Sweep
  $O(n)$ adds
  $O(n)$ swaps

减少加法操作次数？

Stream Compaction

类似于std::copy_if

在GPU的时候我们就把不要的数据给丢了，这样最终需要从GPU传到CPU的
数据量就少了很多。

Why scan?

• Preserve the order
• meet certain criteria

Step 1: Compute temporary array containing

• 1 if corresponding element meets criteria
• 0 if element does not meet criteria

Step 2 Run exclusive
scan on temporary array

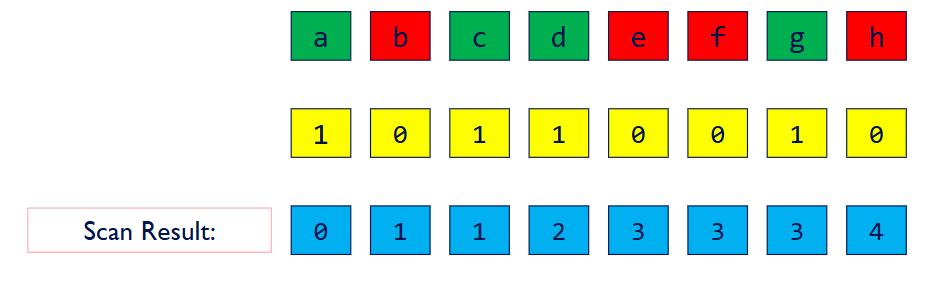
这里第一行是原始数据，绿色表示满足了条件，红色表示未满足条件

黄色是临时数组

蓝色是临时数组的开扫描

Step 3 Scatter

• Results of scan is index into final array
• Only write an element if temporary array has a 1

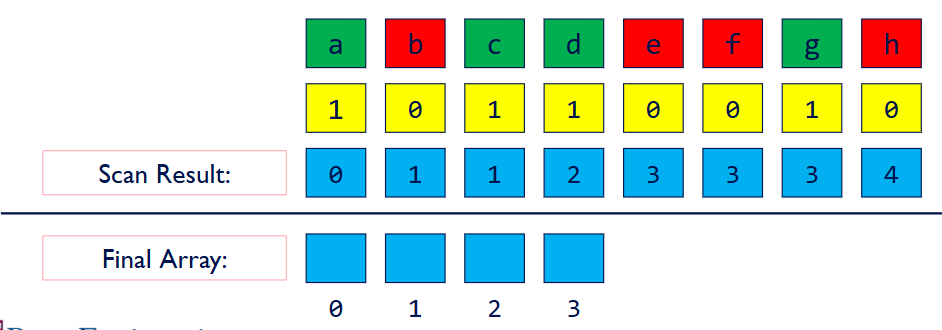
那么利用这个开扫描，我们可以知道要开一个多大的数组，也就是最后一位值，且知道每一个要写的元素将会写的index

Summed Area Table （SAT）

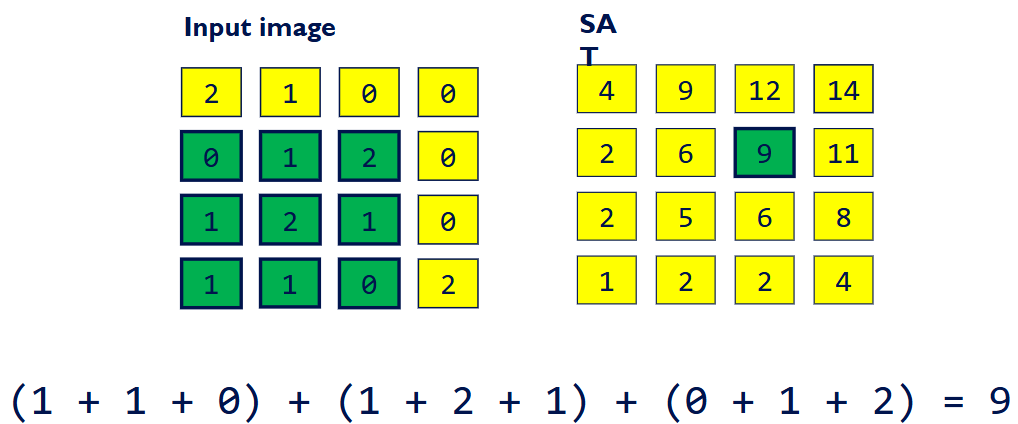
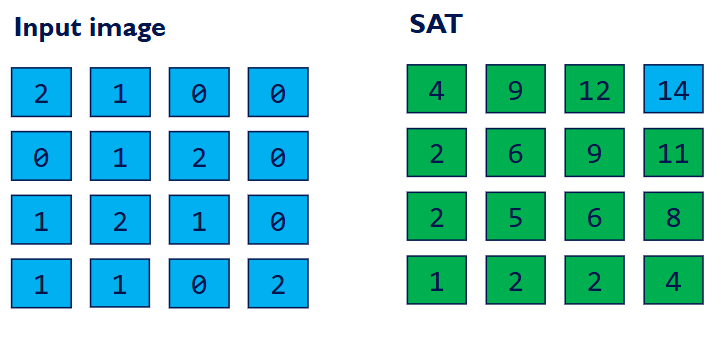
2D table where each element stores the sum of all elements in an input image between the lower left corner and the entry location.

SAT的本质是一个二维的包含式前缀和。

通过一次预计算，使得我们可以在“固定的时间”内，极速计算出图像中任意矩形区域内所有像素值的总和（以及平均值）

它的最大优点是，可以用 固定的时间O(1) 对图像的每个像素应用任意尺寸的矩形滤镜。即计算一个 3x3 小方框内所有像素的平均值，和计算一个 500x500 巨大方框内像素的平均值，花费的时间是完全相同的。

我们不需要遍历矩形内的每一个像素。我们只需要从一个预先计算好的“和区域表（SAT）”中，读取四个角点的值即可。

$$
s_{filter} = \frac{s_ur - s_ul - s_lr + s_ll}{w \times h}
$$

SAT(D) - SAT(B) - SAT(C) + SAT(A)

以近似景深为例
1.对于屏幕上的每一个像素，我们读取它的深度值。
2. 根据深度值和预设的焦距，计算出这个像素应该有多“糊”。这个模糊程度可以直接转换成一个矩形模糊窗口的尺寸（比如5x5, 15x15等）
3. 利用SAT，我们只需4次查询，就能立刻得到这个动态尺寸的矩形窗口内的像素平均值。
5. 将这个平均值作为该像素的最终颜色

GPU Implementation Inclusive Scan

1. 原始输入

[ 1, 2, 3 ]
[ 4, 5, 6 ]
[ 7, 8, 9 ]

2. 水平扫描
   我们对图像的每一行，独立地执行一次包含式扫描
   第1行: [1, 1+2, 1+2+3] ➔ [ 1, 3, 6 ]

第2行: [4, 4+5, 4+5+6] ➔ [ 4, 9, 15 ]

第3行: [7, 7+8, 7+8+9] ➔ [ 7, 15, 24 ]

即

[ 1,  3,  6 ]
[ 4,  9, 15 ]
[ 7, 15, 24 ]

3. 垂直扫描
   我们对上一步得到的中间结果的每一列，再次独立地执行一次包含式扫描

第1列: [1, 1+4, 1+4+7] ➔ [ 1, 5, 12 ]

第2列: [3, 3+9, 3+9+15] ➔ [ 3, 12, 27 ]

第3列: [6, 6+15, 6+15+24] ➔ [ 6, 21, 45 ]

// 最终的 SAT
[  1,  3,  6 ]
[  5, 12, 21 ]
[ 12, 27, 45 ]

Radix Sort

k-bit keys require k passes k比特的键需要k轮处理

如果要对一个k比特的整数进行排序，算法需要进行k轮

1. (Pass 1)根据所有数字的最低比特位 least significant bit (LSB)（第0位是0还是1）进行分组排序
   

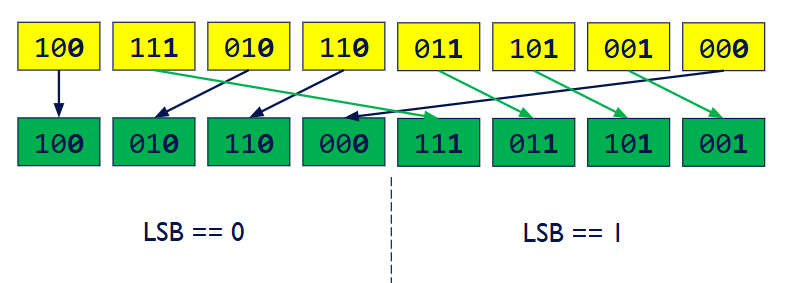
2. (Pass 2)在上一轮结果的基础上，根据所有数字的次低比特位（第1位）进行分组排序
   

3. ….

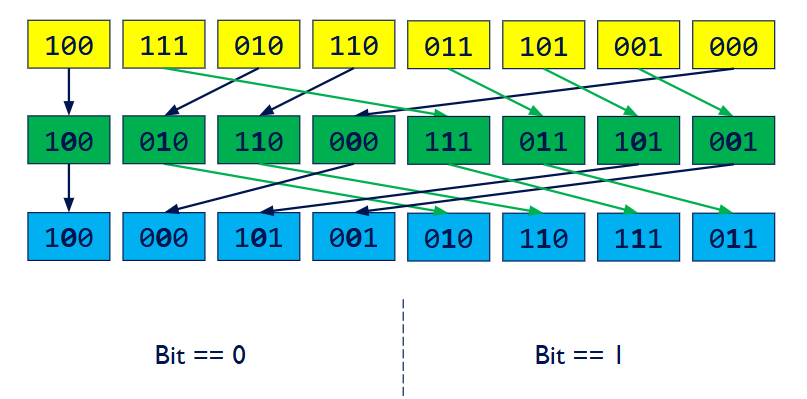
4. (Pass k)根据最高比特位most significant bit (MSB)
   

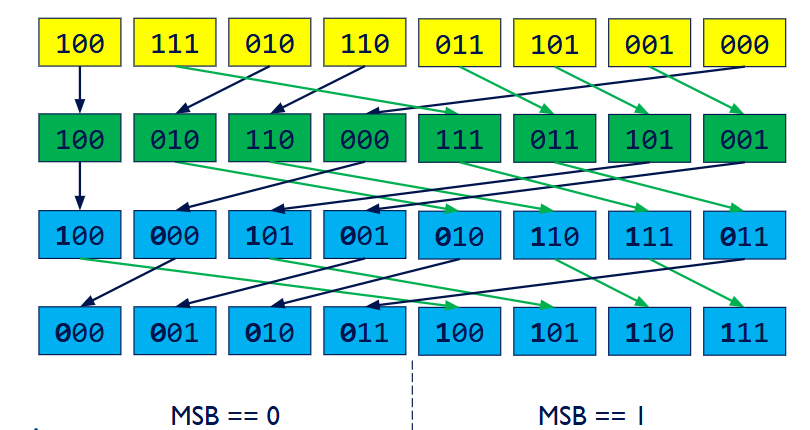
Parallel ?

1. Break input arrays into tiles

   • Each tile fits into shared memory for an SM

2. Sort tiles in parallel with radix sort

   • Each pass is done in sequence after the previous pass. No parallelism
   • Can we parallelize an individual pass? How?

3. Merge pairs of tiles using a parallel bitonic merge until all tiles are merged.

Parallel in a pass

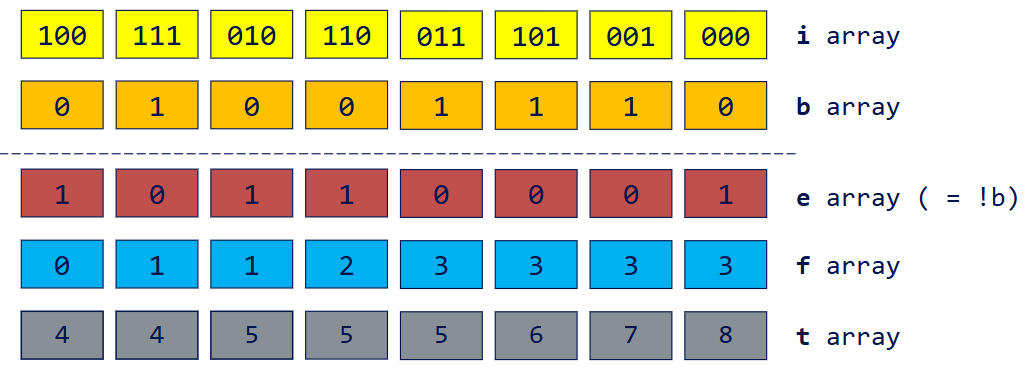
1. 计算 e 数组
   
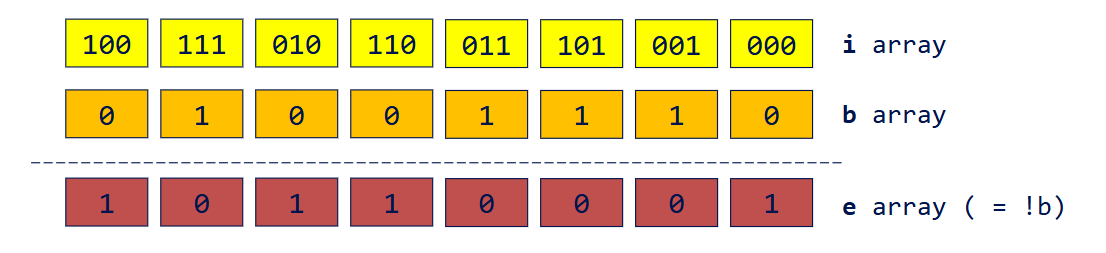
2. 对 e 数组执行开扫描
   
3. 计算 totalFalses

totalFalses = e[n – 1] + f[n – 1]
totalFalses = 1 + 3
totalFalses = 4

4. Compute t array

• t array is address for writing true keys

totalFalses = 4
t[i] = i – f[i] + totalFalses

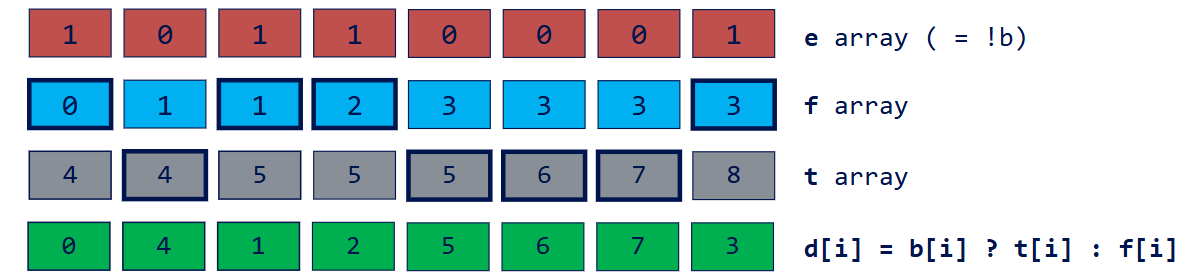
5. Scatter based on address d

d[i] = b[i] ? t[i] : f[i] 

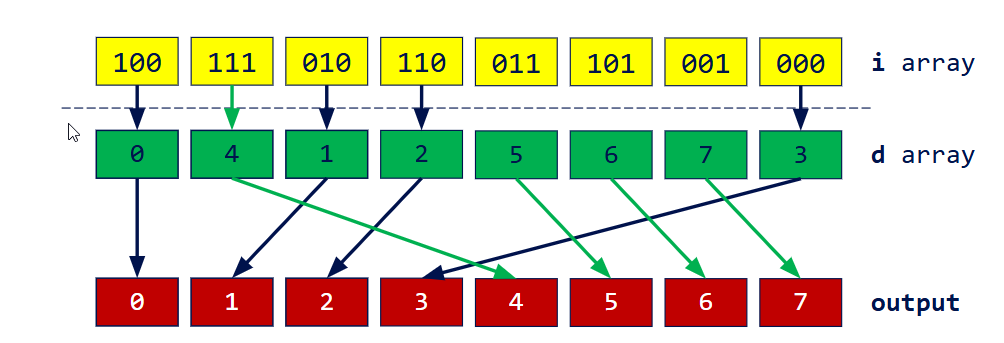
算法将相邻的两个有序数据块（Tile 0 和 Tile 1，Tile 2 和 Tile 3，以此类推）两两配对。

GPU上的不同线程组会同时对这些数据块对执行并行的归并操作

Scan Revisited

• Limitations
  • Requires power-of-two length
  • Executes in one block (unless only using global memory)
    • Length up to twice the number of threads in a block

1. Devide the array into blocks
2. Run scan on each block
   
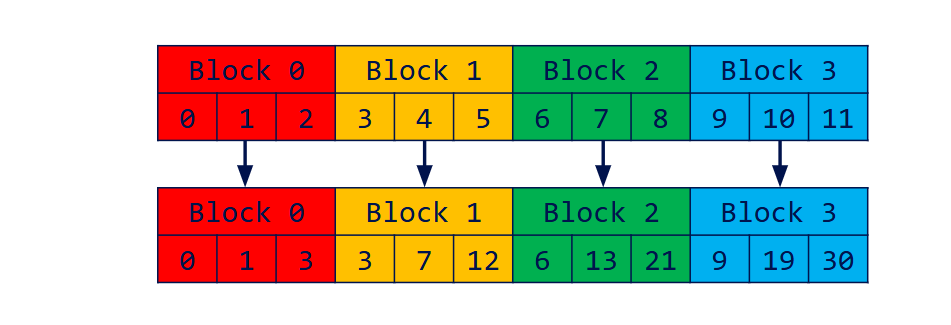
3. Write total sum of each block into a new array
   
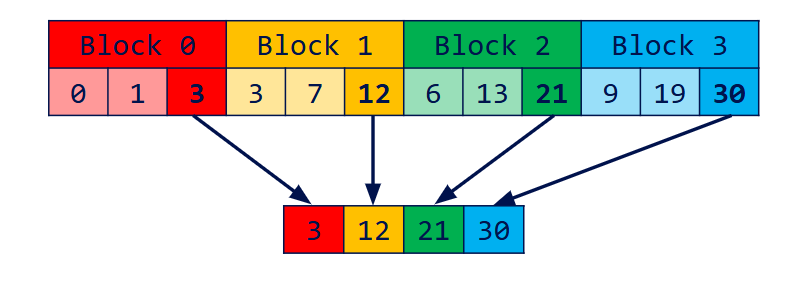
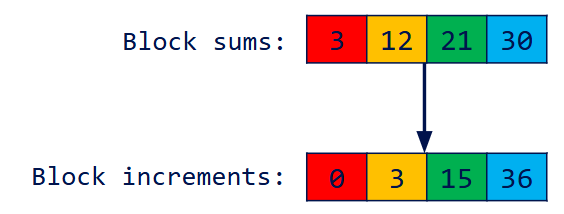
4. Exclusive scan block sums to compute block increments
   
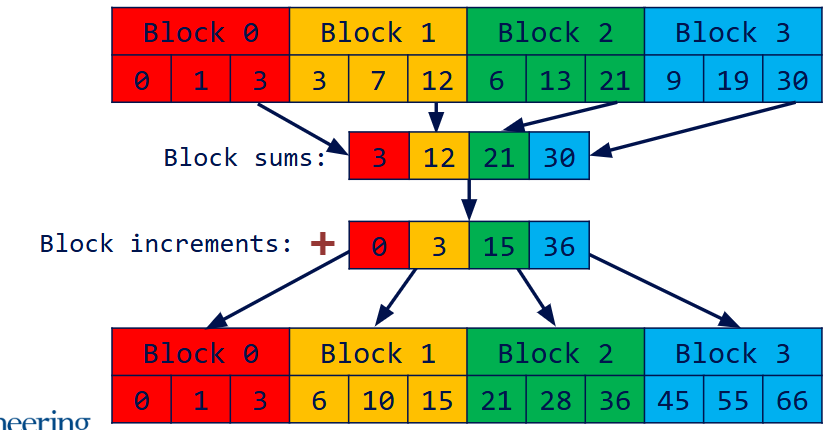
5. Add block increments to each element in the corresponding block