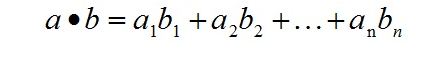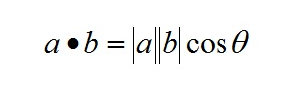Refer to: The Continuity of Splines by Freya Holmér

• Bernstein

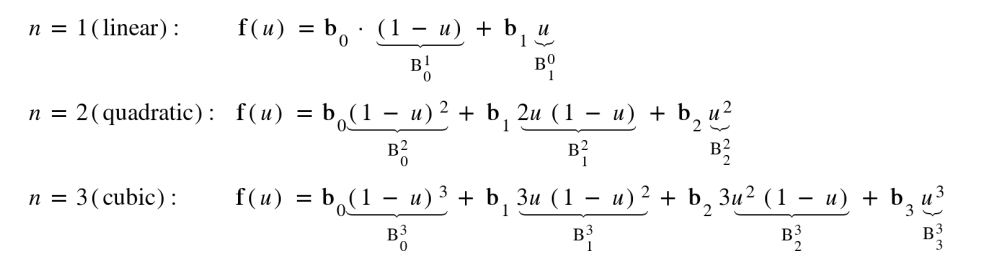
此处，$B_0^{3}$ 等亦可写作 $B_{0,3}(u) = C(3,0) \cdot u ^{0} \cdot (1-u)^{3}$

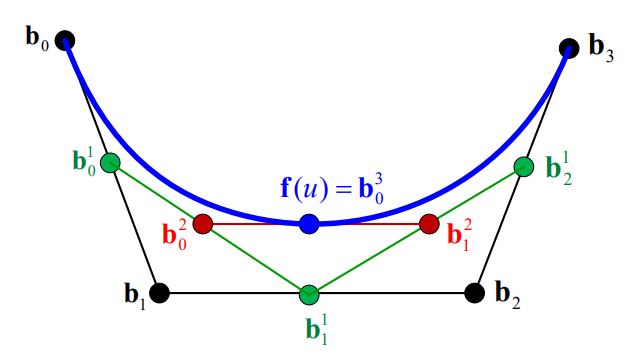
• DeCasteljau

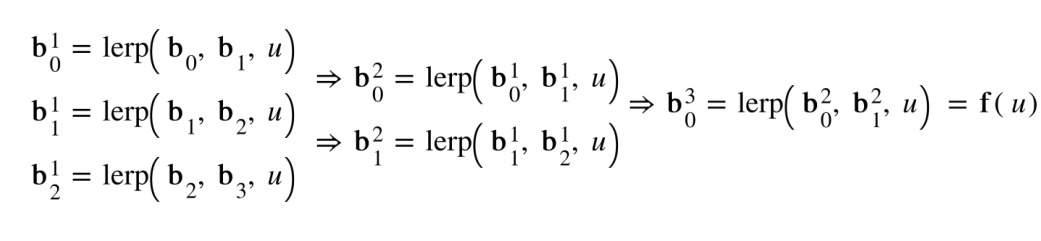
• Polynomial Coefficients
  $$
  f(u) = b_0 + u(-3b_0 + 3b_1) + u^{2}(3b_0 -6b_1 + 3b_2) + u^{3}(-b_0 + 3b_1 -3b_2 + b_3)
  $$
  Efficient Evaluation using Horner’s Method：
  $$
  f(u) = C_0 + u(C_1 + u(C_2 + uC_3))
  $$

Subdivision of Bezier Curve

Derivatives of Bezier Curves

For the case where u = 0

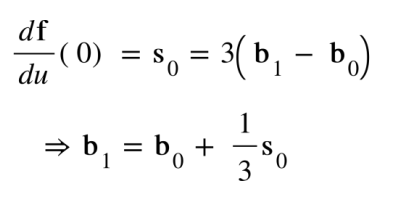
when u = 1

Why Spline？

如果需要我们对一条曲线有更多的控制能力，我们可以考虑提高贝塞尔曲线的次数，例如，一个6次贝塞尔曲线会有7个控制点，其形如：
$$
X(s) = (1-s)^6 P_0 + 6s(1-s)^5 P_1 + 15s^2(1-s)^4 P_2 + 20s^3(1-s)^3 P_3 + 15s^4(1-s)^2 P_4 + 6s^5(1-s) P_5 + s^6 P_6
$$
但是，移动每个控制点的时候，整个曲线都会受到影响，计算也会变得更加复杂。

为了更稳定地计算并获得更好地局部控制线和直观性，我们会将多段较低阶地贝塞尔曲线连接起来。

三种切线

Continuity

$C^{n}$ continuous if $A^{(i)}(t_{end}) = B^{(i)}(t_{start})$ for $i$ in $ {0,…,n}$

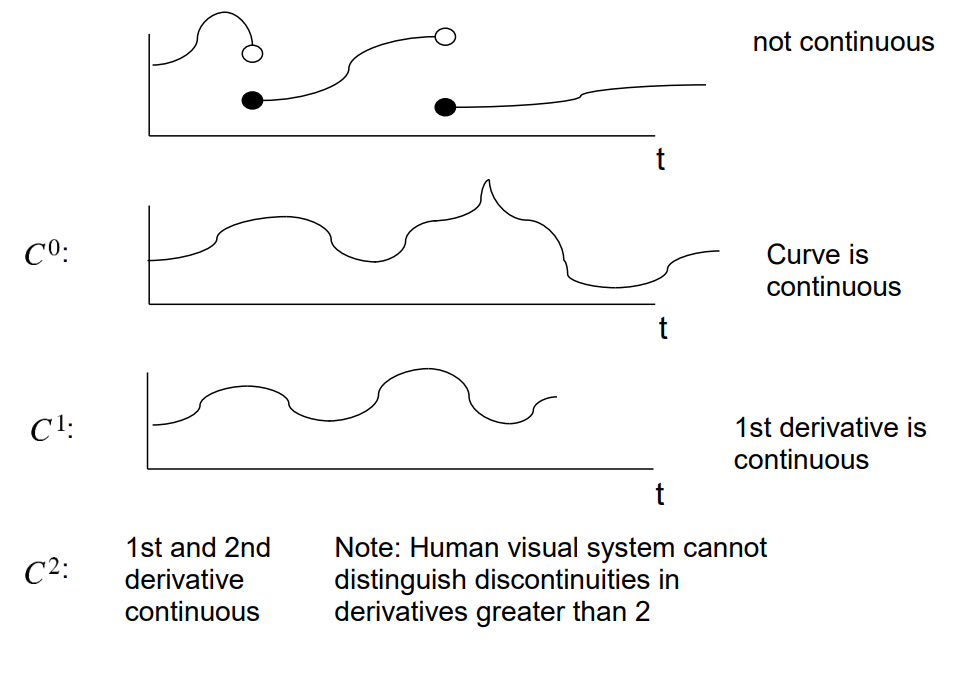
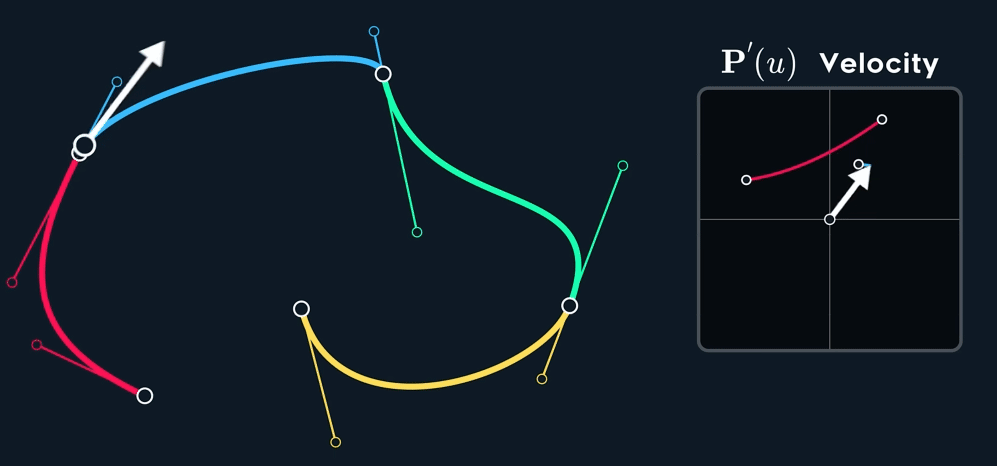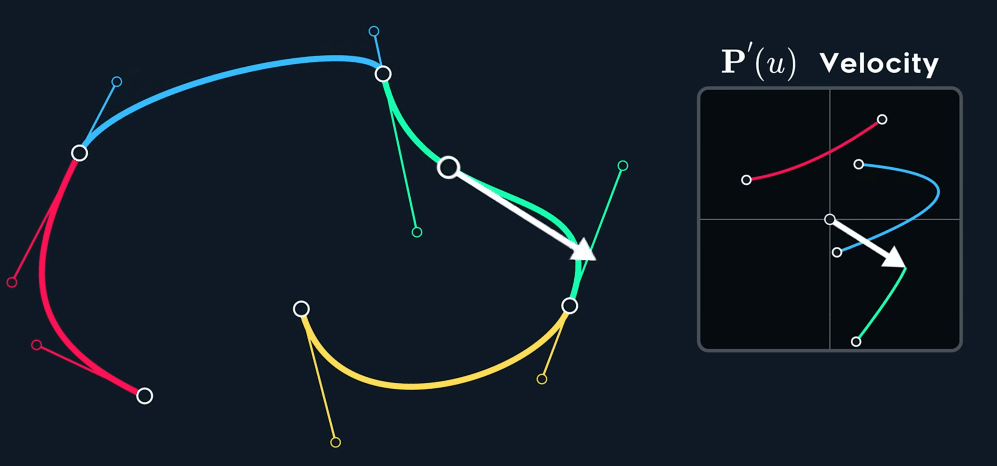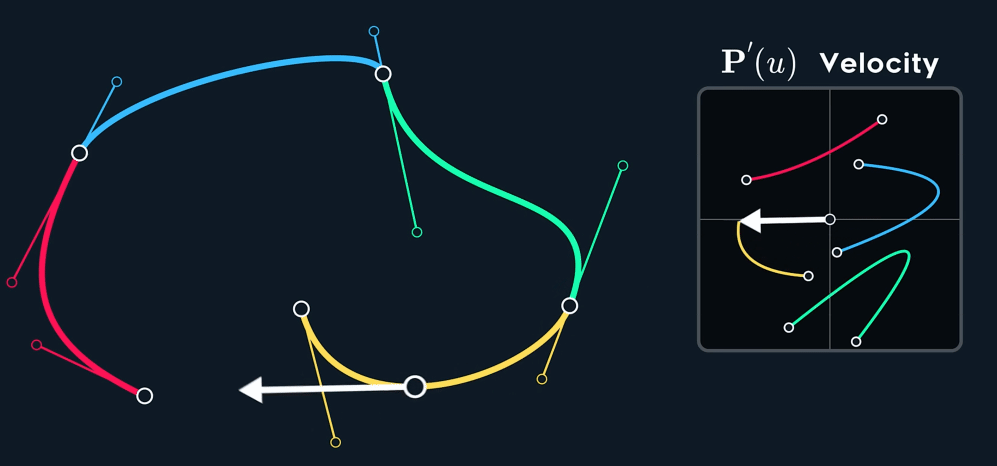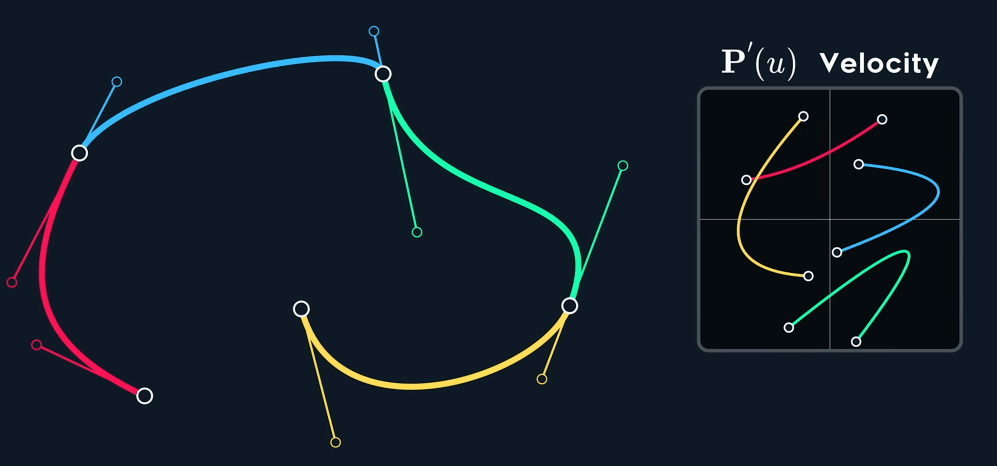
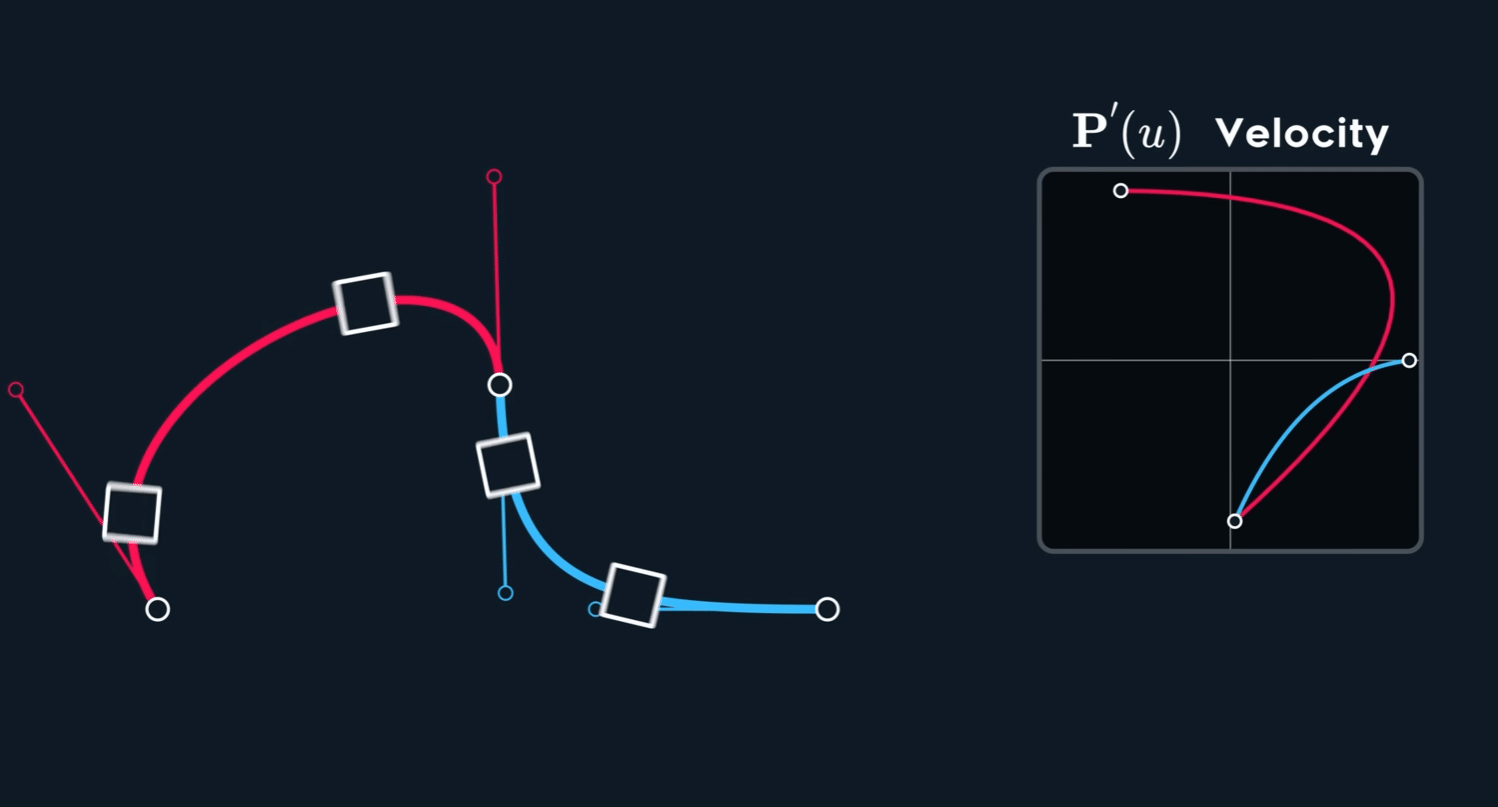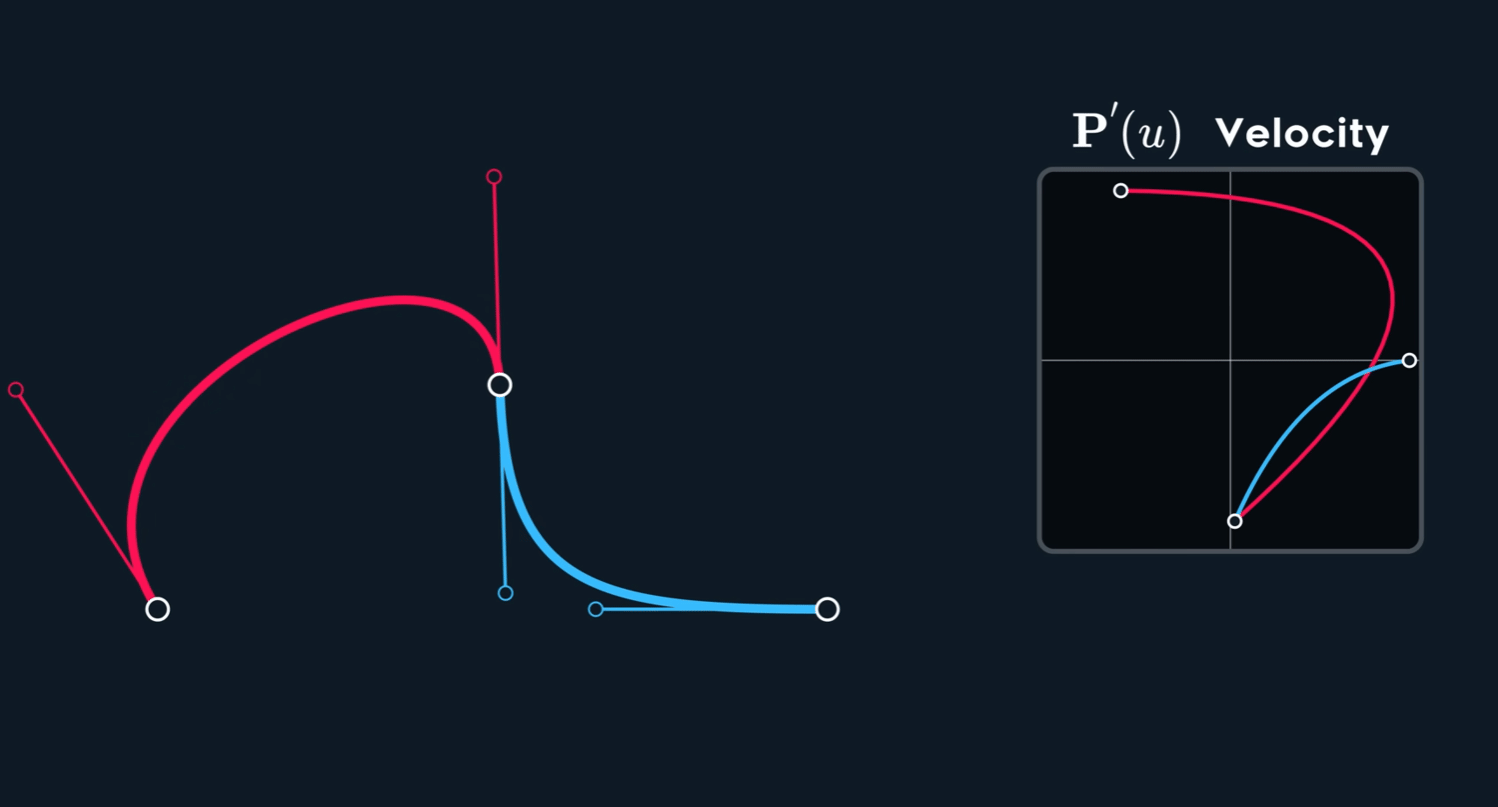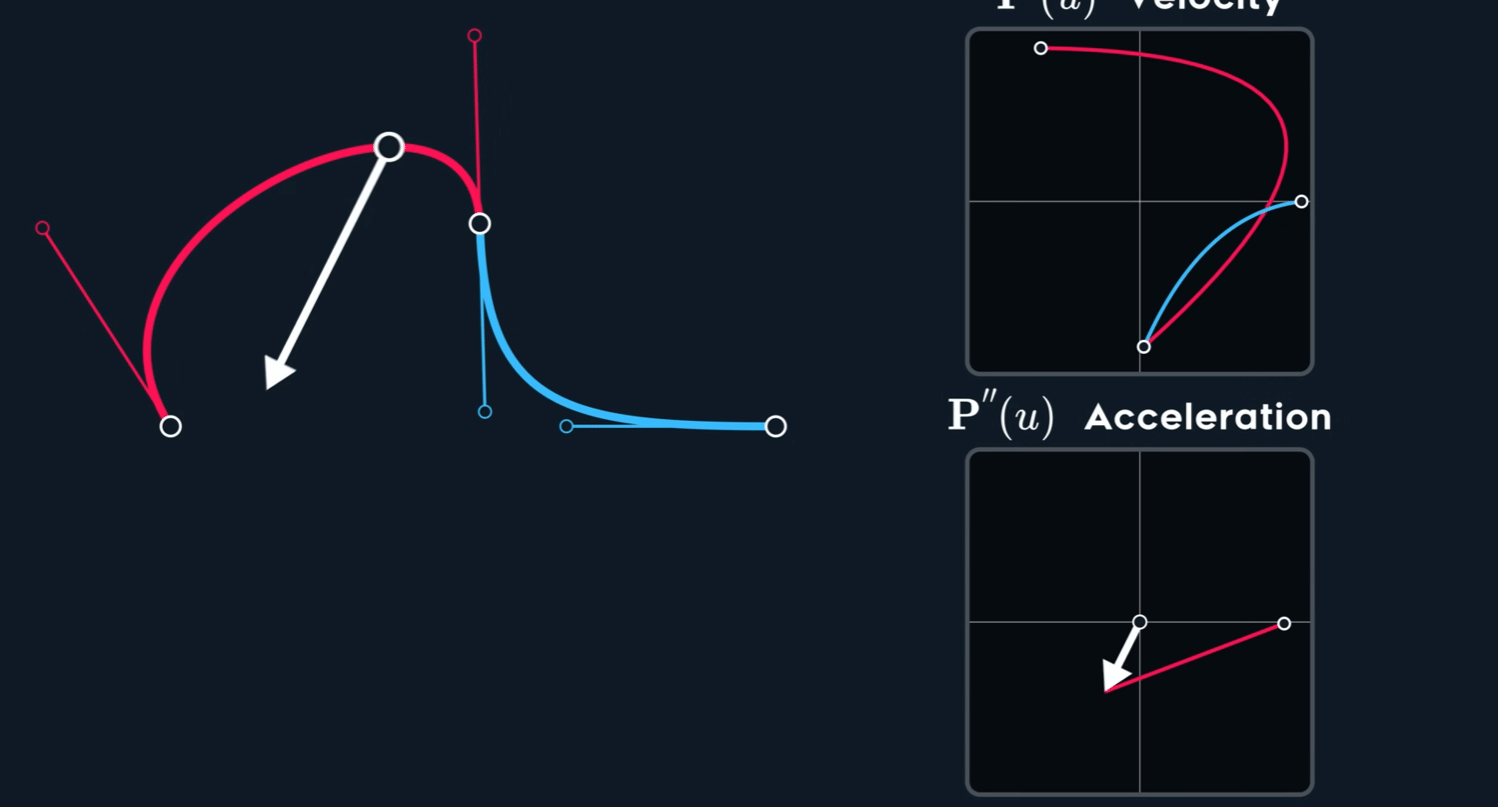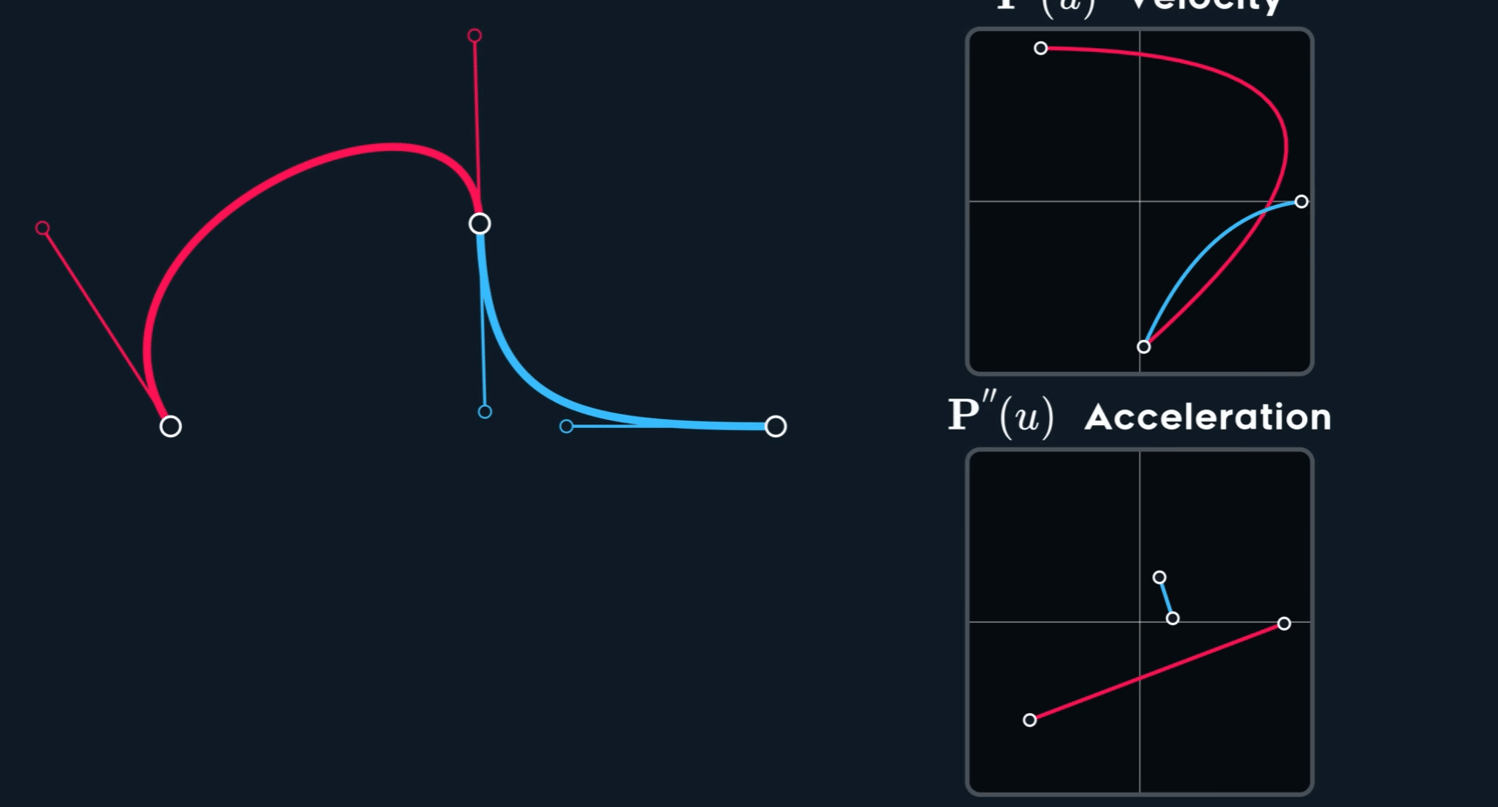
观察下图，可以看到速度并不是连续的，也就是不满足 $C^1$ 连续性。即使原 spline 在 joint 处的两个控制点形成的两个切线已经 aligned (方向相同，但是大小不同)。

当控制点关于 joint 点 mirror 时， $C^1$连续。

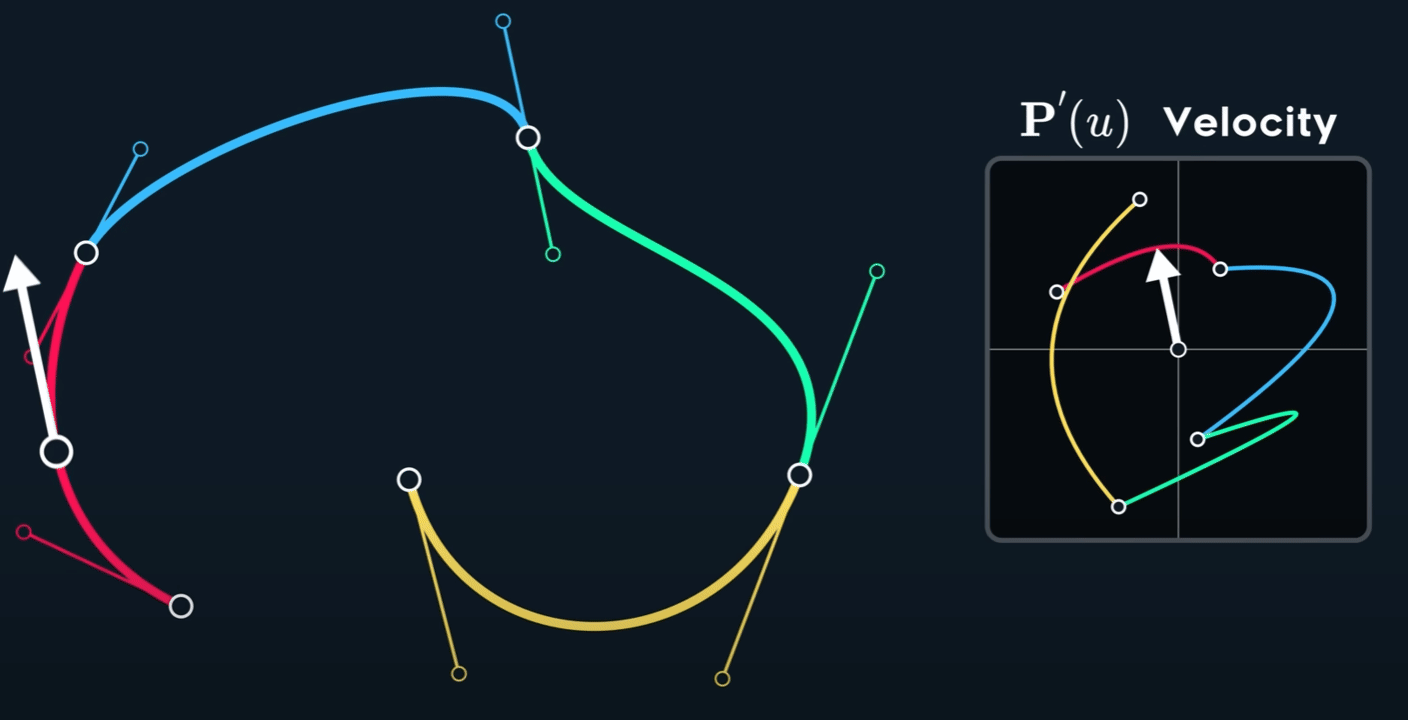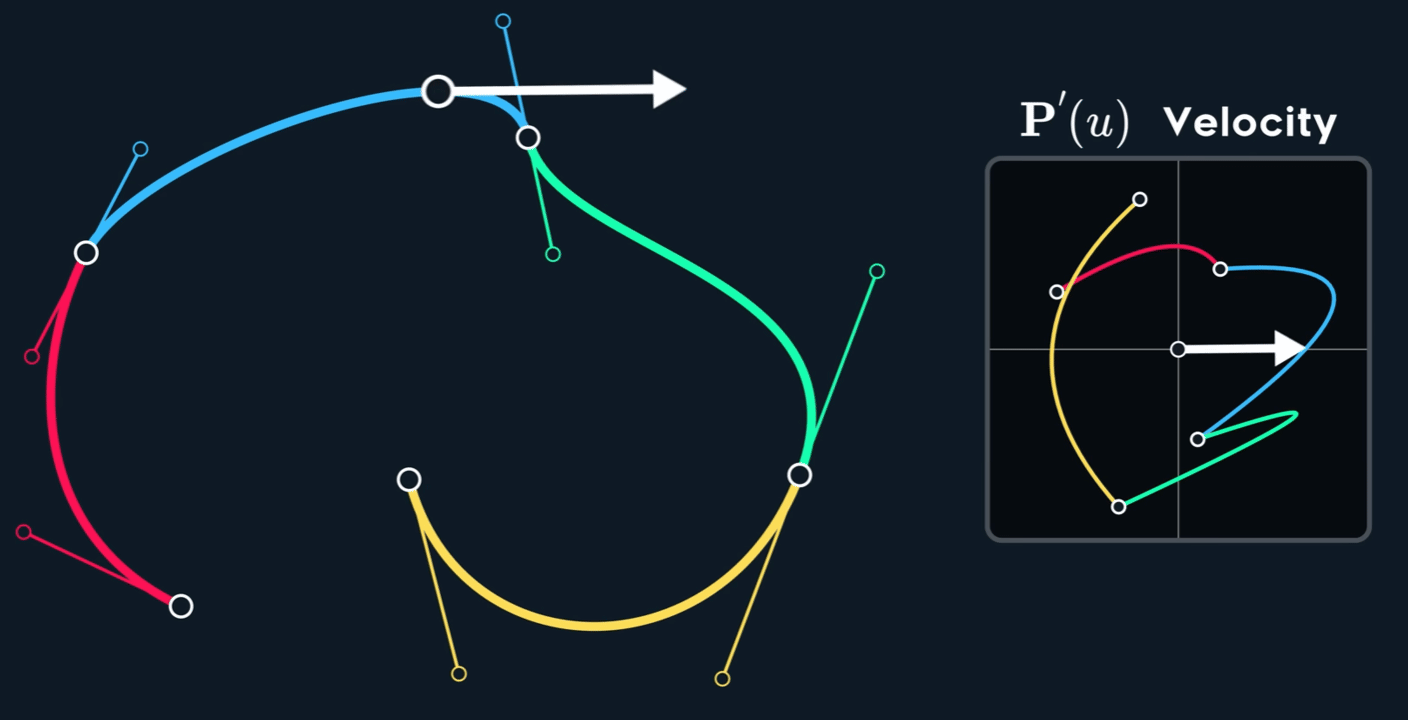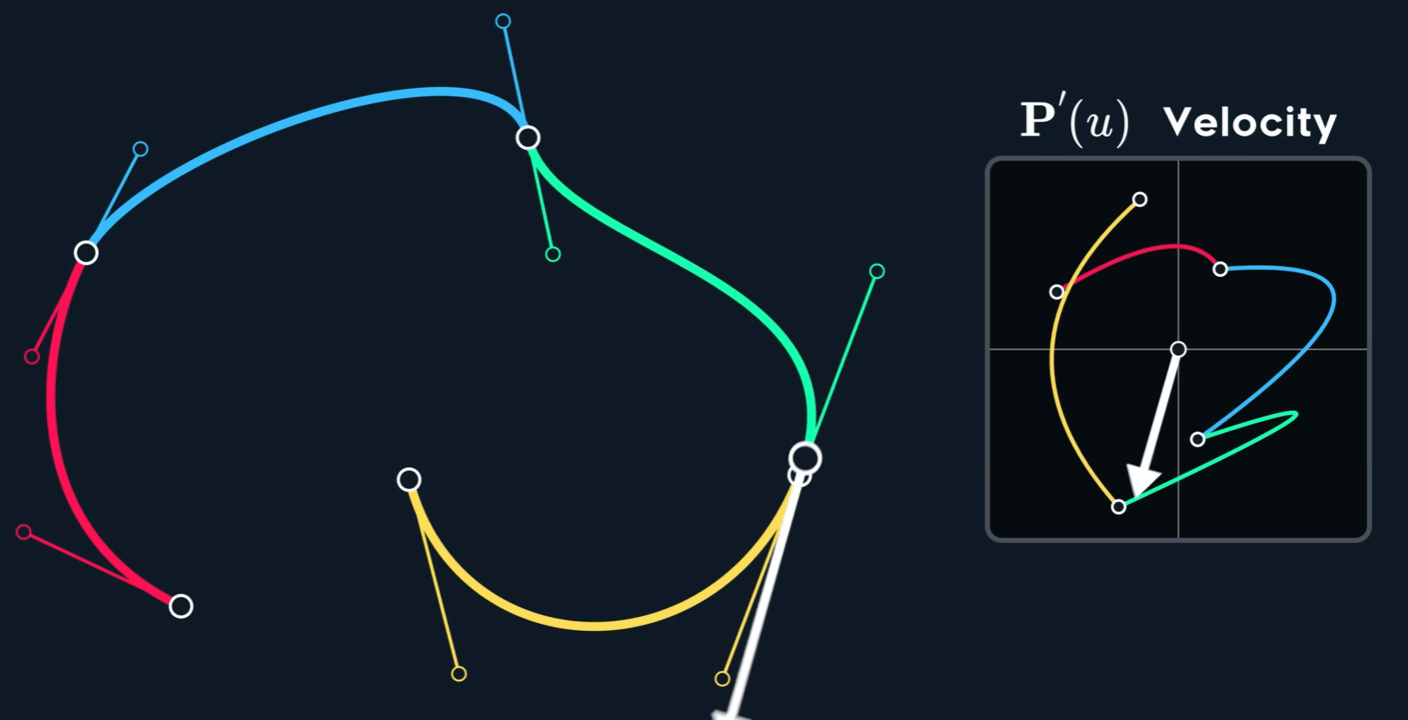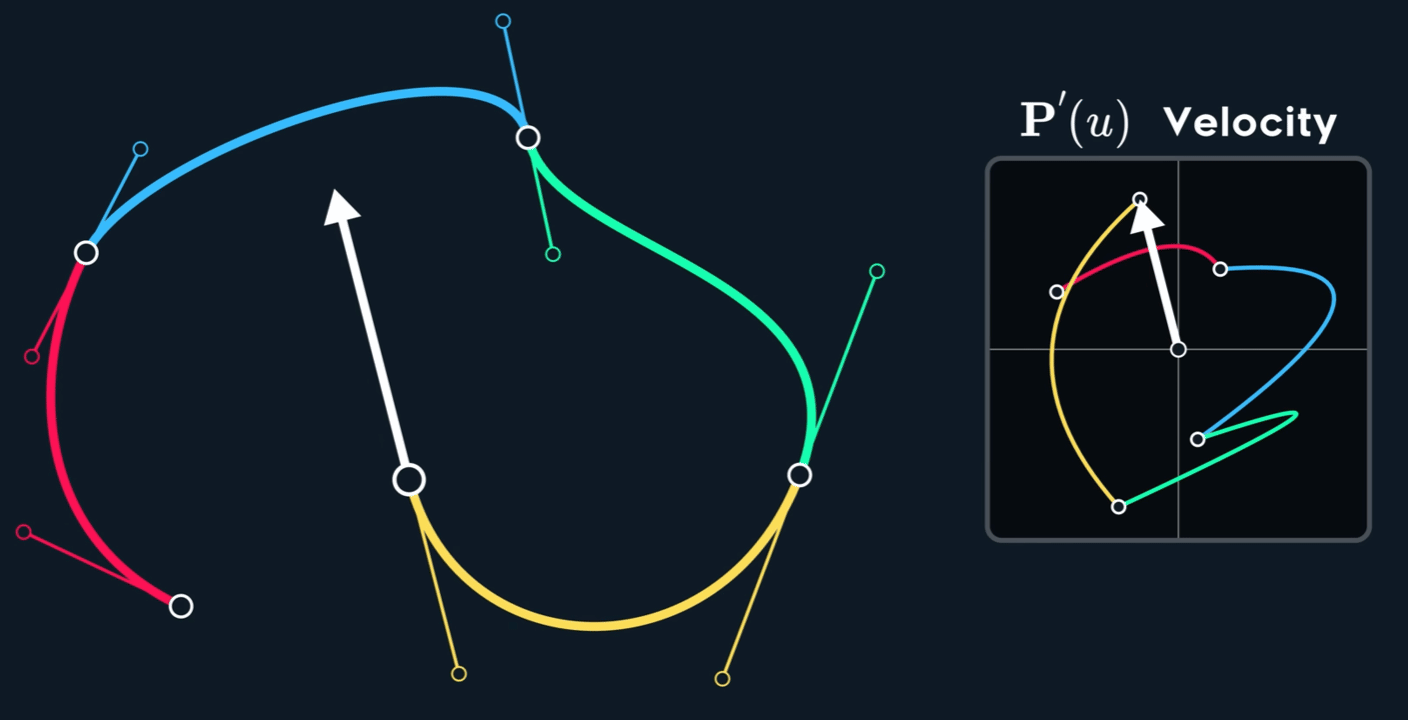
如何构造出 $C^1$ 呢？Mirror 意味着怎么样的关系呢？

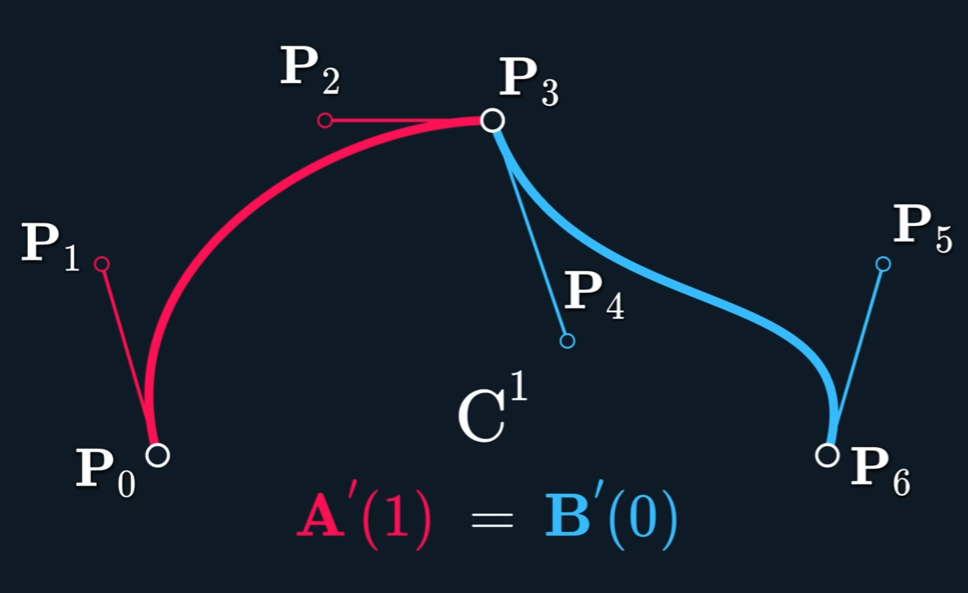
我们对一段贝塞尔曲线求导，有
$$
f’(u) = -3b_0 + 3b_1 + 2u(3b_0 -6b_1 + 3b_2) + 3u^2(-b_0 + 3b_1 -3b_2 + b_3)
$$
那么，当$u_0 = 1$时（第一段曲线的右端点）
$$
f’(1) = -3b_2 + 3b_3
$$
当$u_1 = 0$ （第二段曲线的左端点）
$$
f’(0) = -3b_3 + 3b_4
$$
当$f’(1) =f’(0)$时，有
$$
b_4 = 2b_3 - b_2
$$
也就是说，当 Mirror 时，$b_4$ 的位置已经被 $b_2$ 与 $b_3$ 完全决定，不再能被用户自由控制。

$C^2$ 连续性？

加速度改变速度。

我们对上面提到的速度再求一次导，有
$$
f’’(u) = 6b_0 -12b_1 + 6b_2 + 6u(-b_0 + 3b_1 -3b_2 + b_3)
$$
那么，当$u_0 = 1$时（第一段曲线的右端点）
$$
f’’(1) = 6b_1 - 12b_2 +6 b_3
$$
当$u_1 = 0$ （第二段曲线的左端点）
$$
f’’(0) = 6b_3 -12b_4 + 6b_5
$$
当$f’’(1) =f’(0)$时，有
$$
b_5 = b_1 - 2 b_2 + 2b_4
$$
而$C^{1}$ =又保证了，$b_4$ 已经完全被$b_3$ 与$b_2$ 控制
$$
b_4 = 2b_3 - b_2
$$
所以在$C^{2}$下有
$$
b_5 = b_1 + 4(b_3 - b_2)
$$
也就是说，当 $C^{2}$ 时，$b_5$ 的位置已经被 $b_1$ $b_2$ 与 $b_3$ 完全决定，不再能被用户自由控制。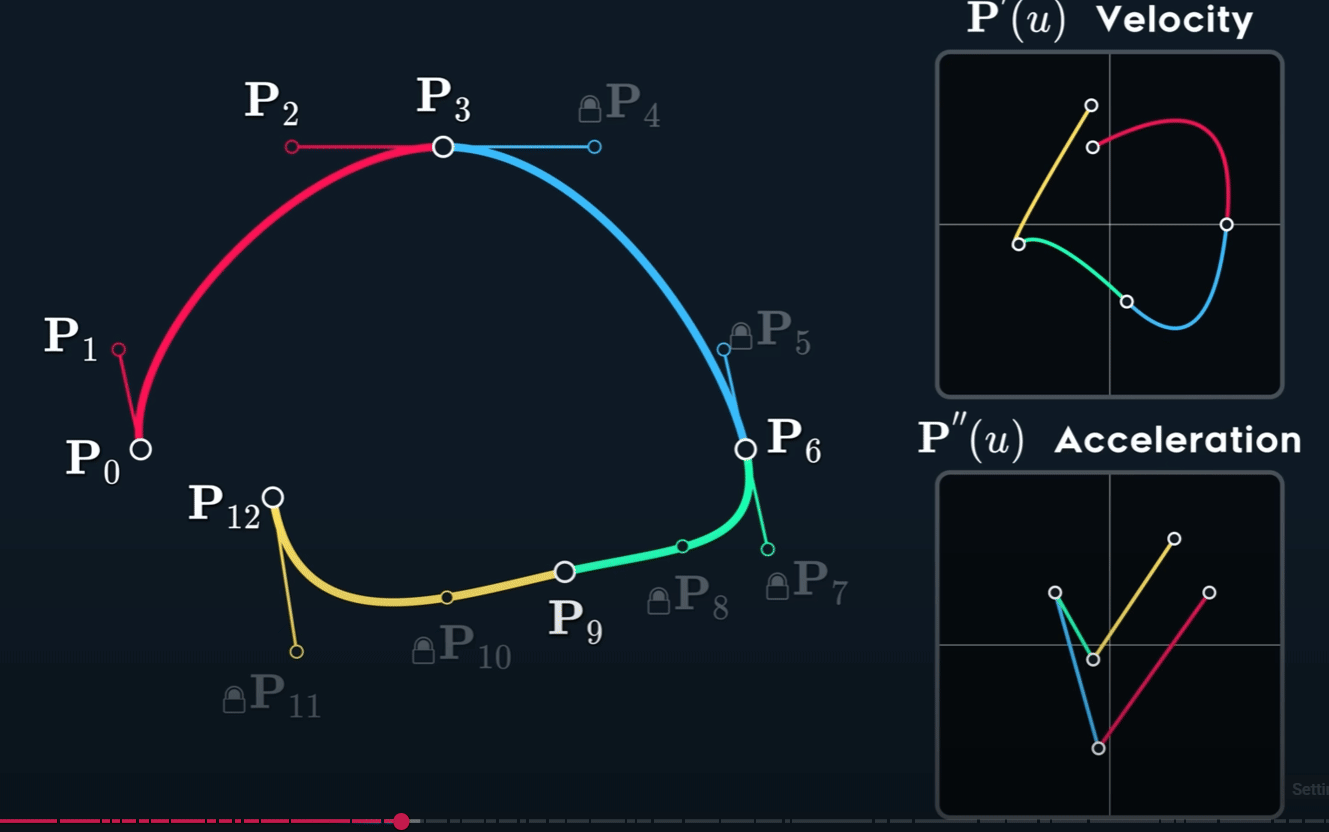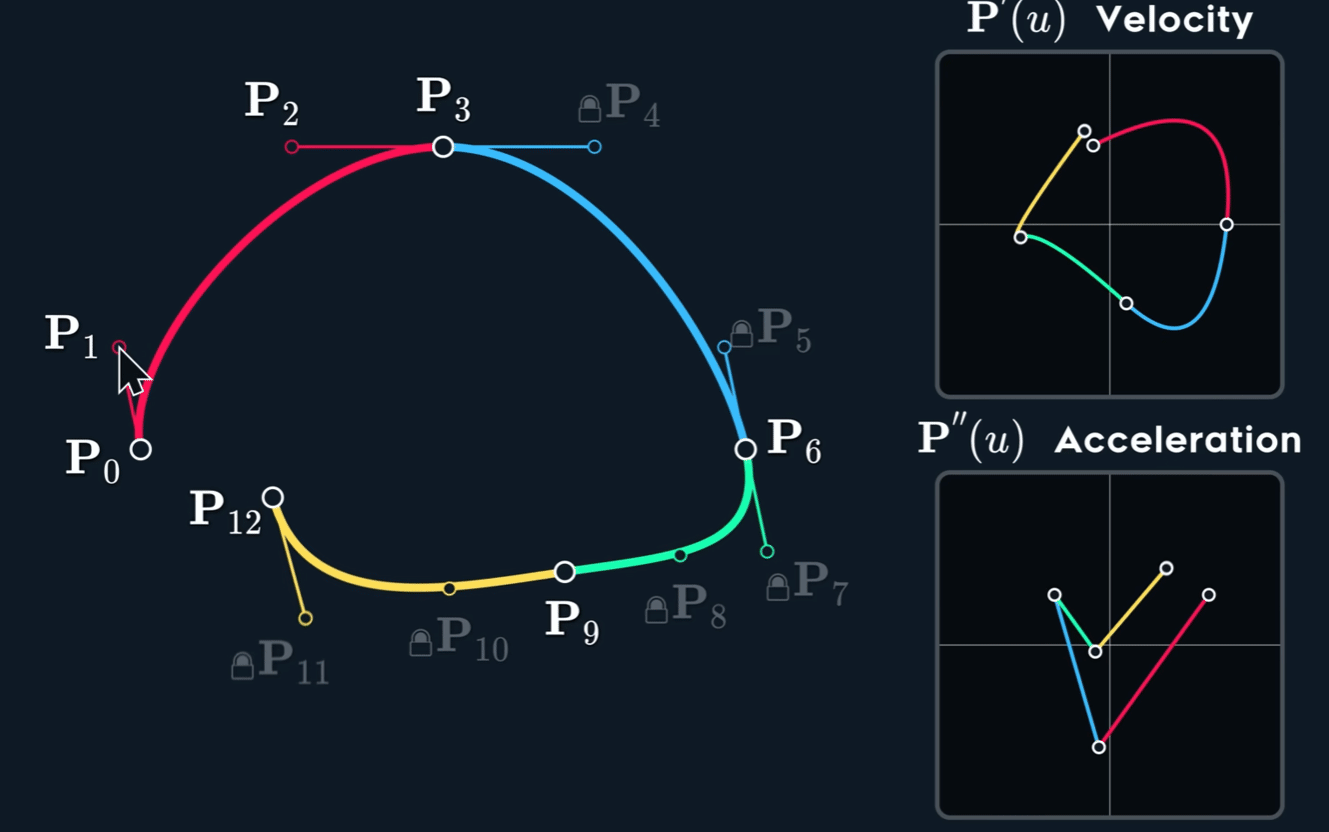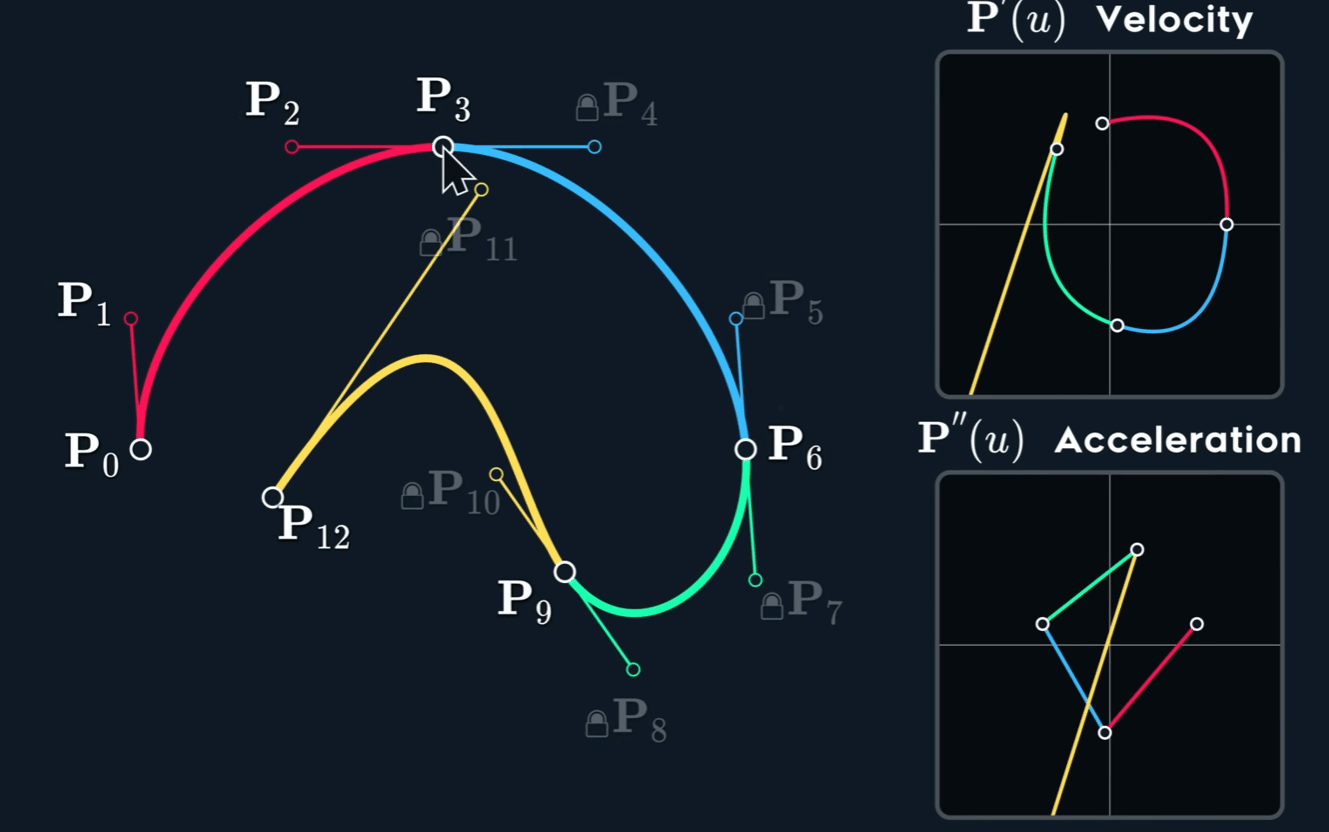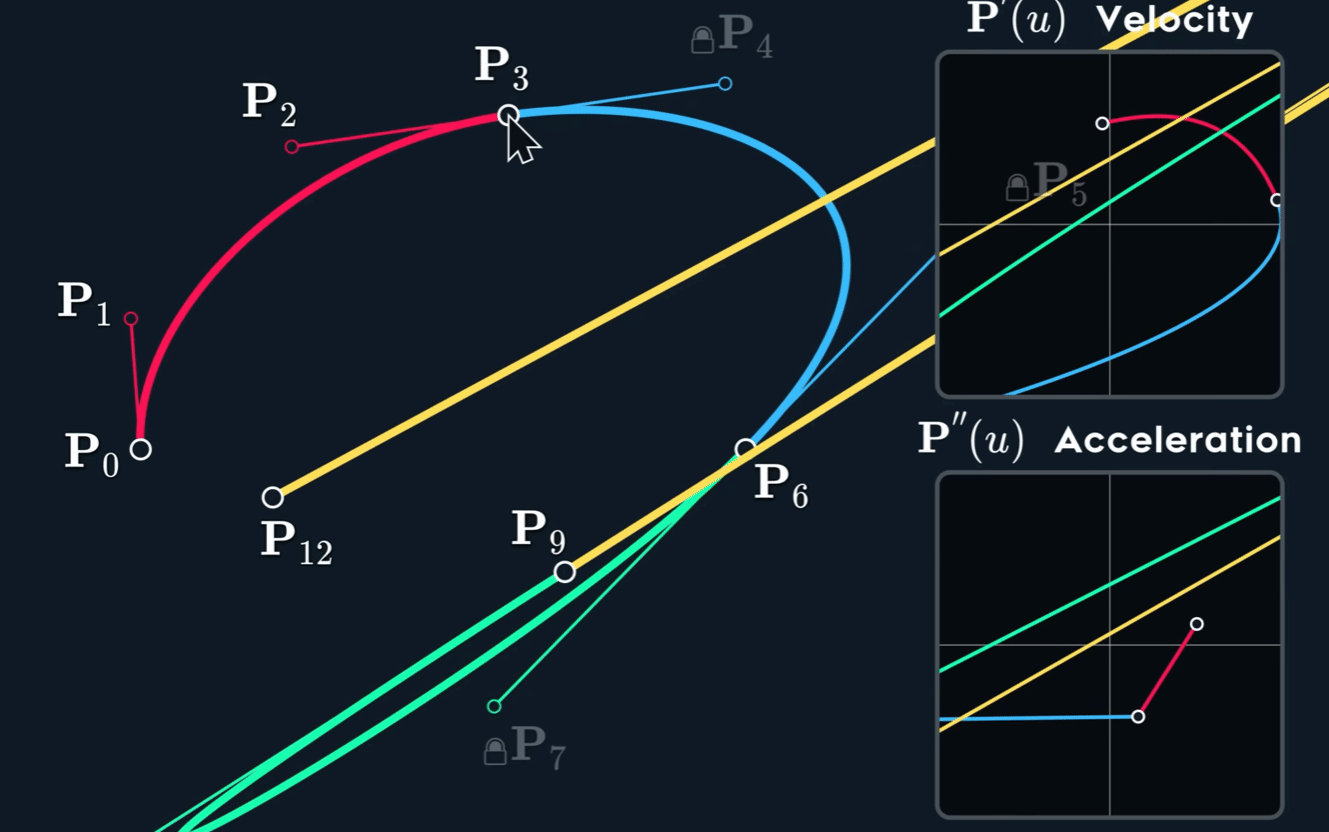

对于多段贝塞尔曲线构成的spline，保证$C^2$时，很多控制点的位置都已经被完全决定，控制能力变弱了，并且， 微小的控制会导致后面剧烈的变化。

Geometric Continuity

$A(t)$ and $B(t)$ are
$G^n$ ccontinuous if a function $g(t)$ exists so that $A(t)$ and $B(g(t))$ are $C^{n}$ continuous

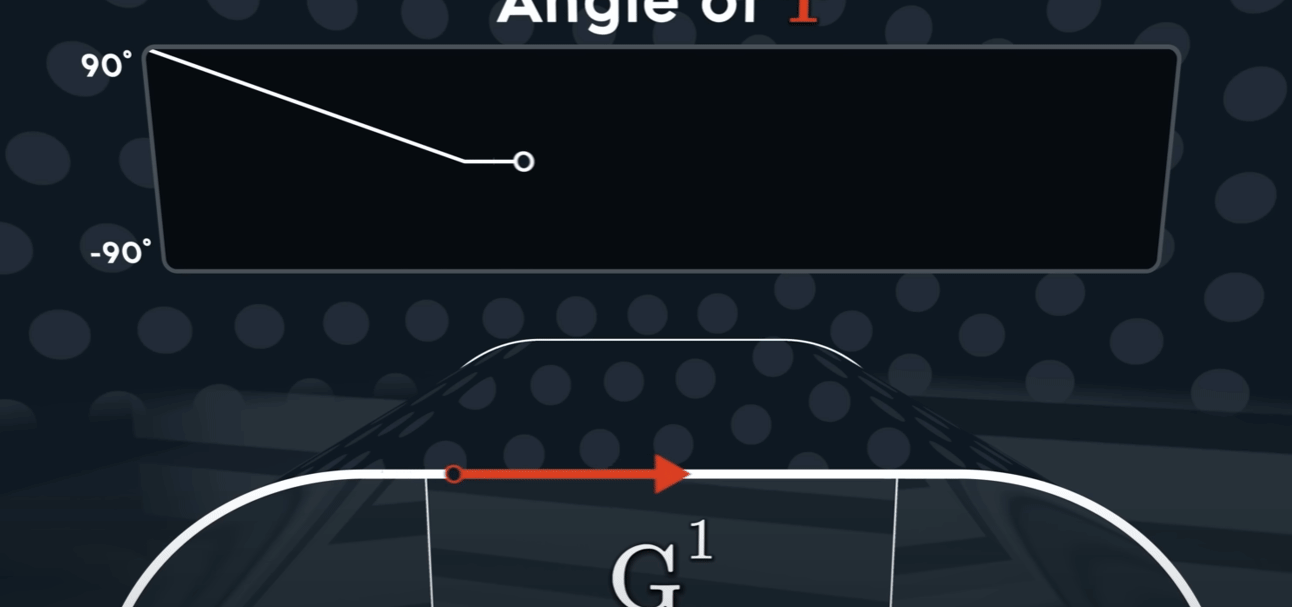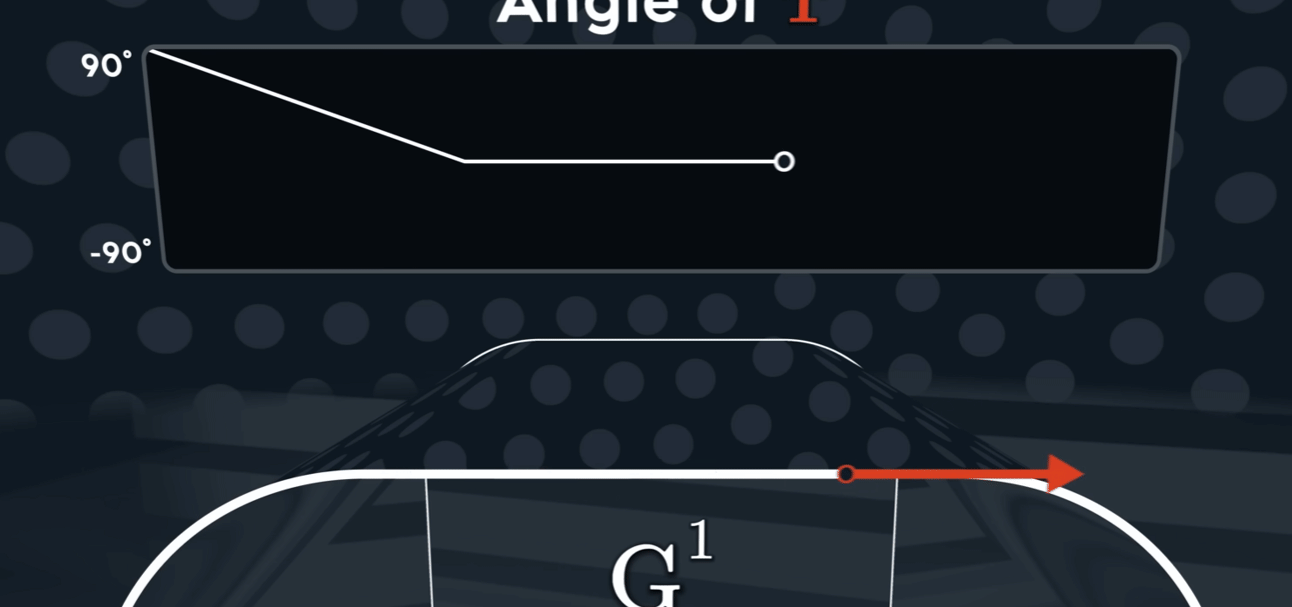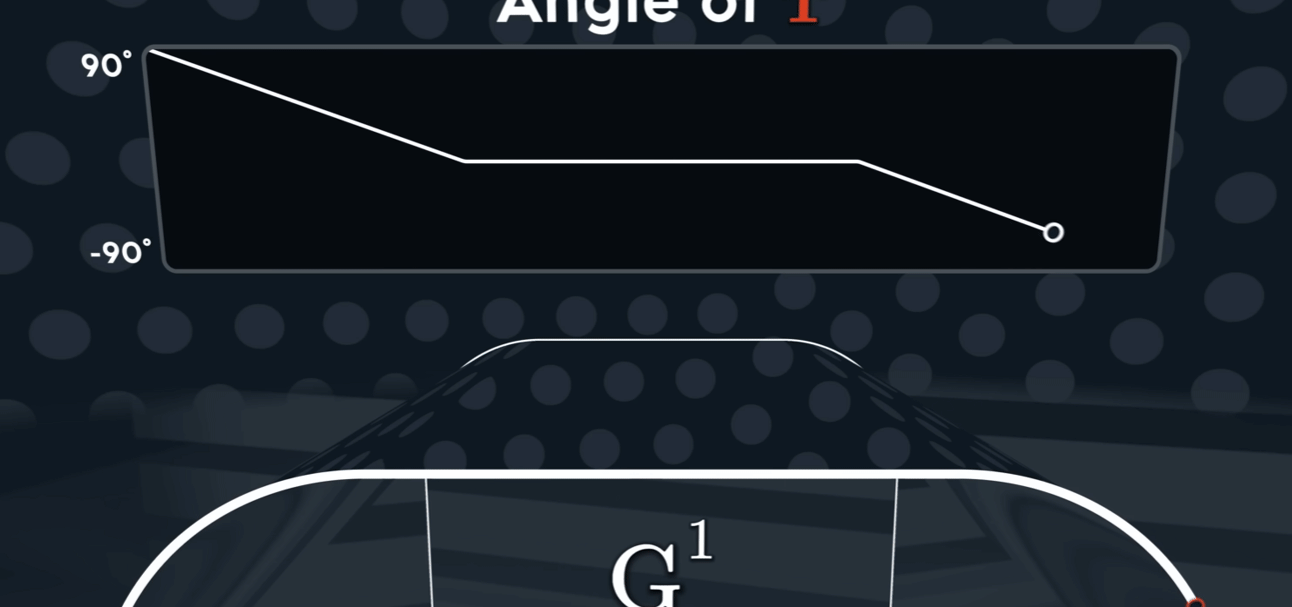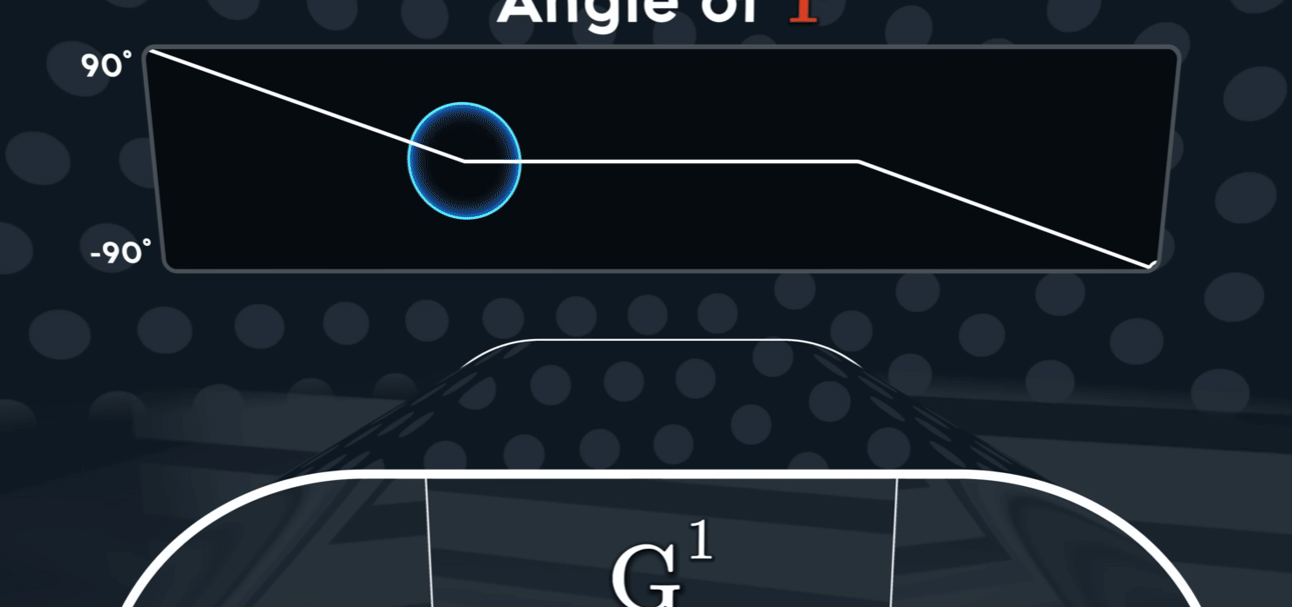
$G^{1}$

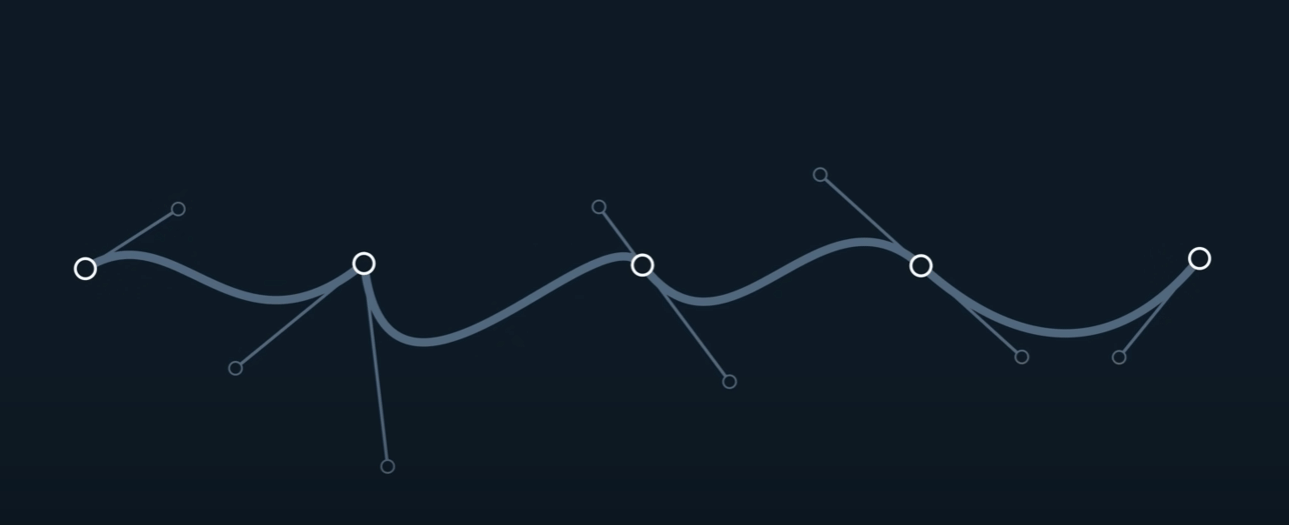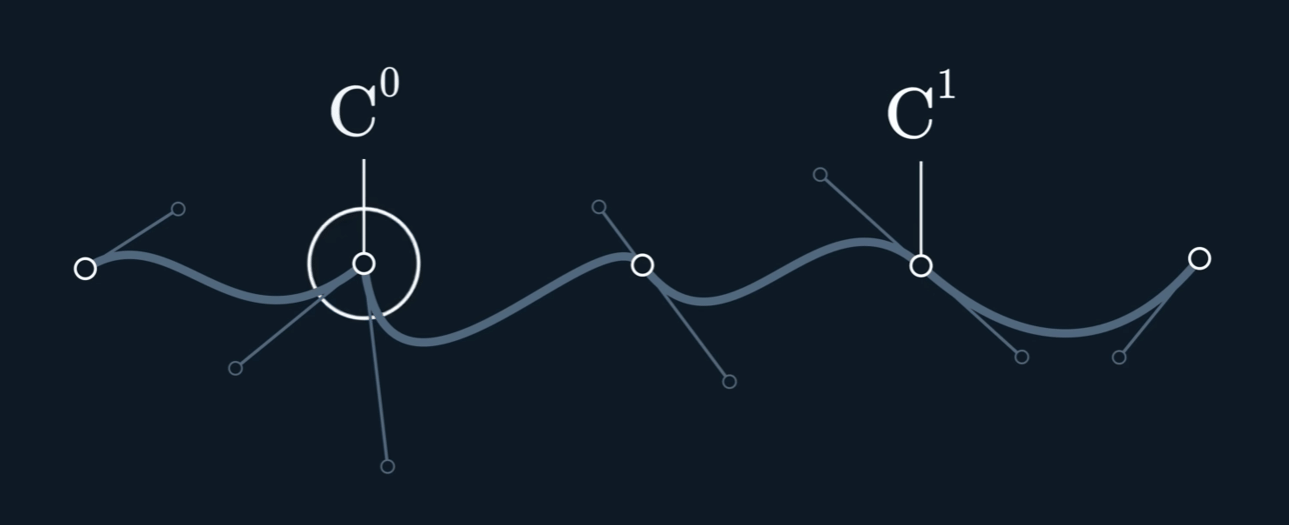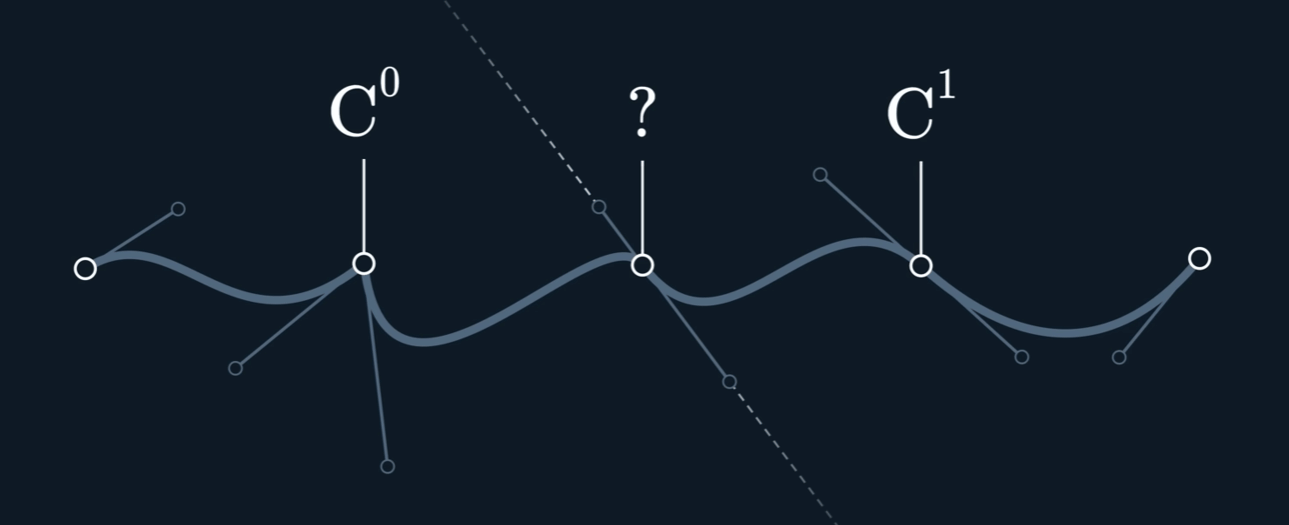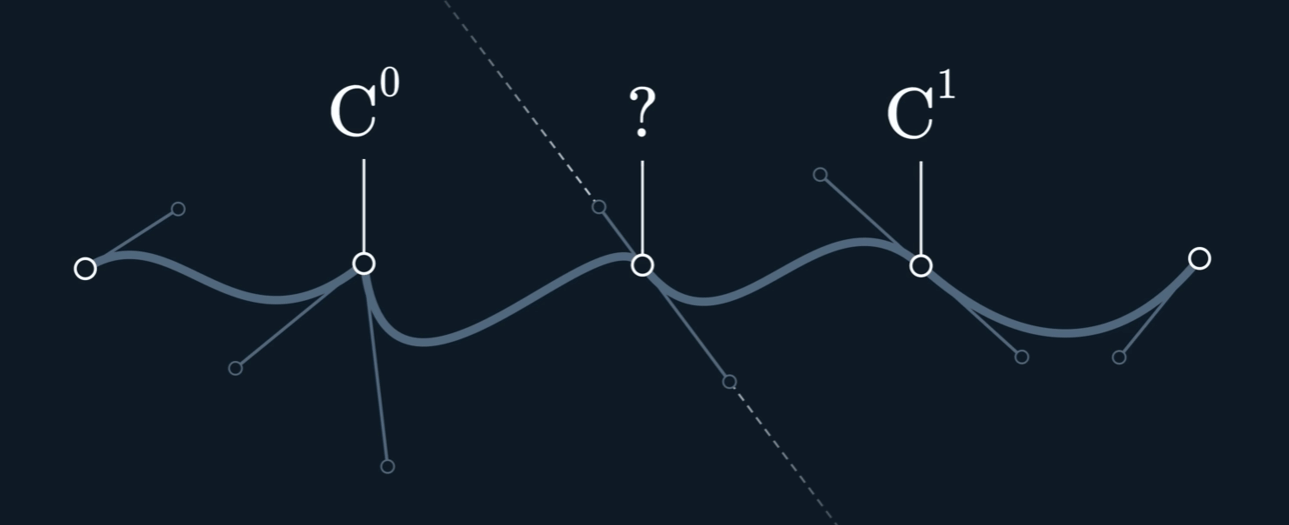
切线连续性通常用 G¹ 连续性 (Geometric Continuity, first-order) 来表示。为了让两条曲线在连接点处达到 G¹ 连续，必须满足以下两个条件：

G⁰ 位置连续性 (Positional Continuity): 两条曲线的端点必须在连接点处重合。也就是说，它们必须接触。

切线方向相同: 在连接点处，两条曲线的切线向量必须指向相同的方向（或者完全相反的方向，但在实际应用中通常要求方向一致）。这意味着两条曲线在该点的变化趋势是一致的。
值得注意的是，G¹ 连续性只要求切线的方向相同，而不要求切线向量的大小（即参数导数的大小）也相同。如果切线向量的大小和方向都相同，那么就达到了更高级别的 $C^1$ 参数连续性 (Parametric Continuity, first-order)。 $C^1$ 连续性是比 G¹ 更严格的条件

满足 $G^{1}$ 时，有
$$
b_4 = b_3 + (b_3 - b_2) \beta
$$
即，共线同向，但不要求大小相同。

在曲面上，我们可以注意到反光有条缝

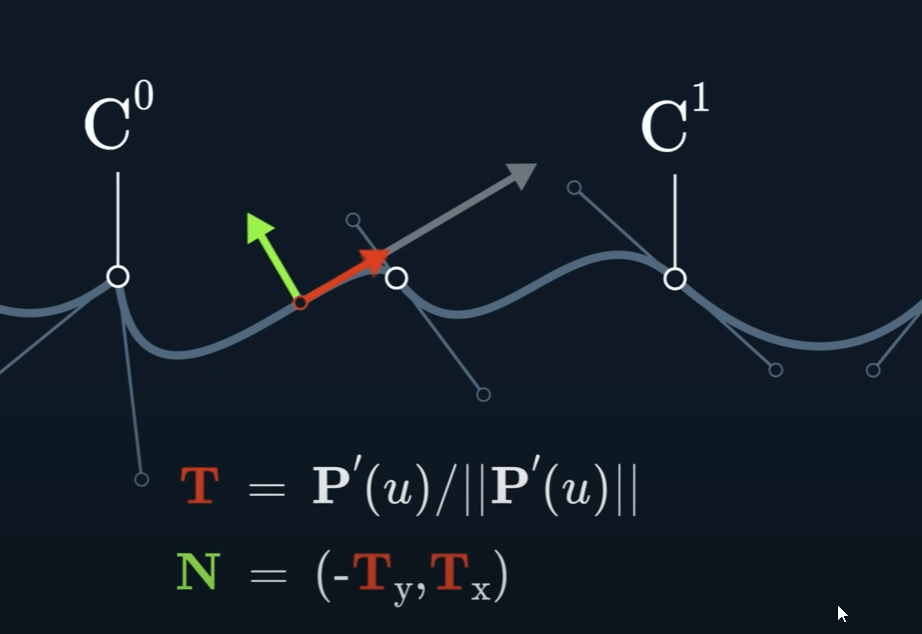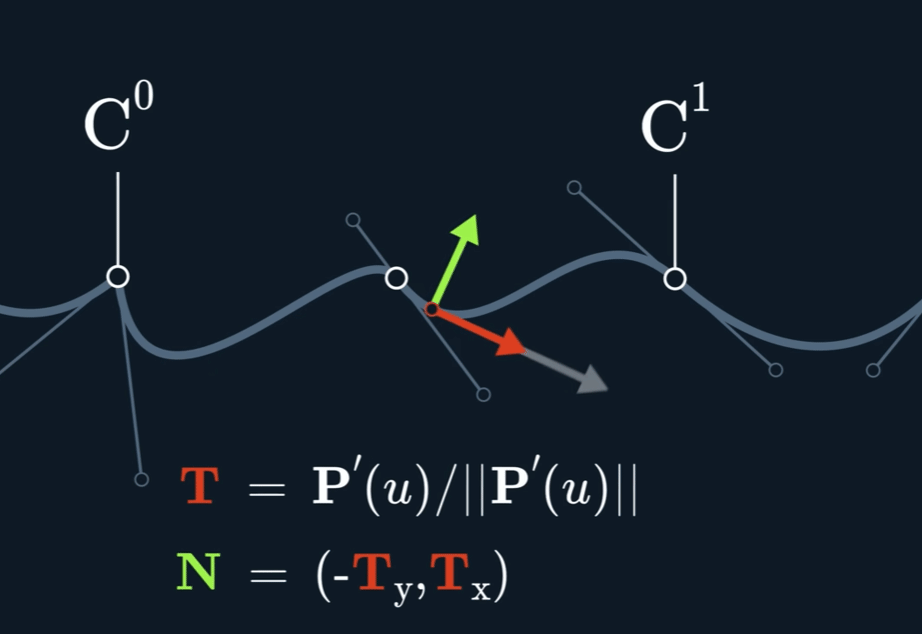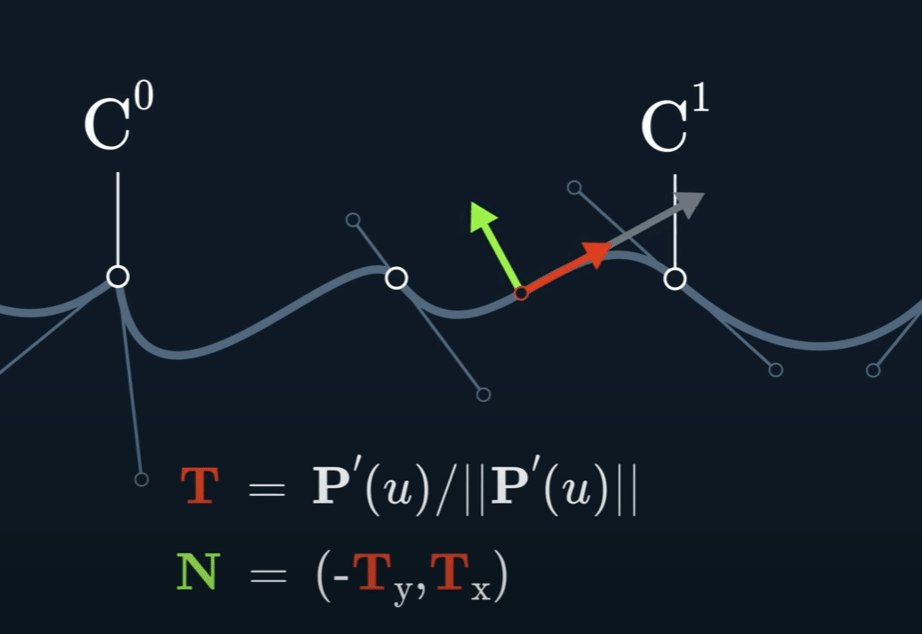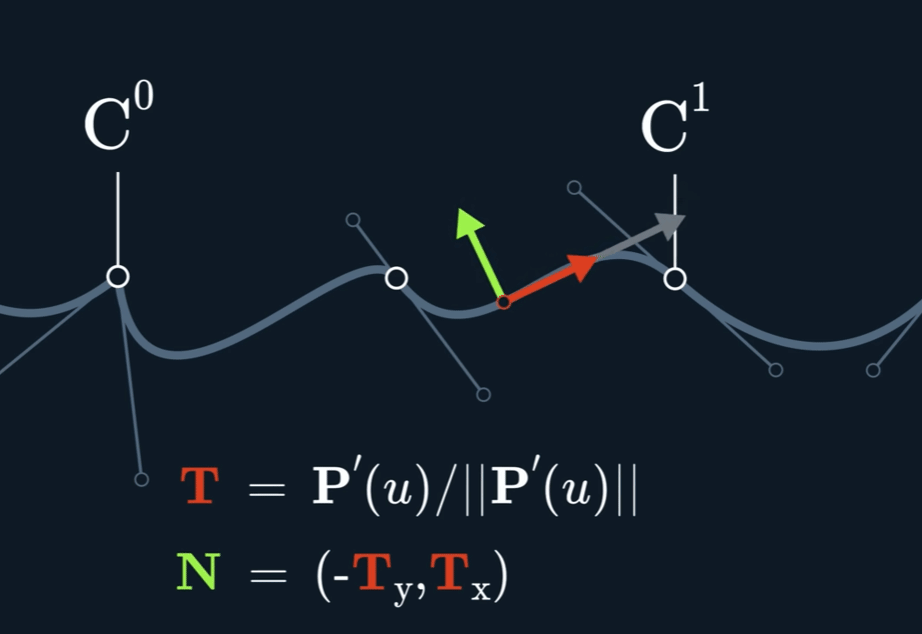
Curvature $k$

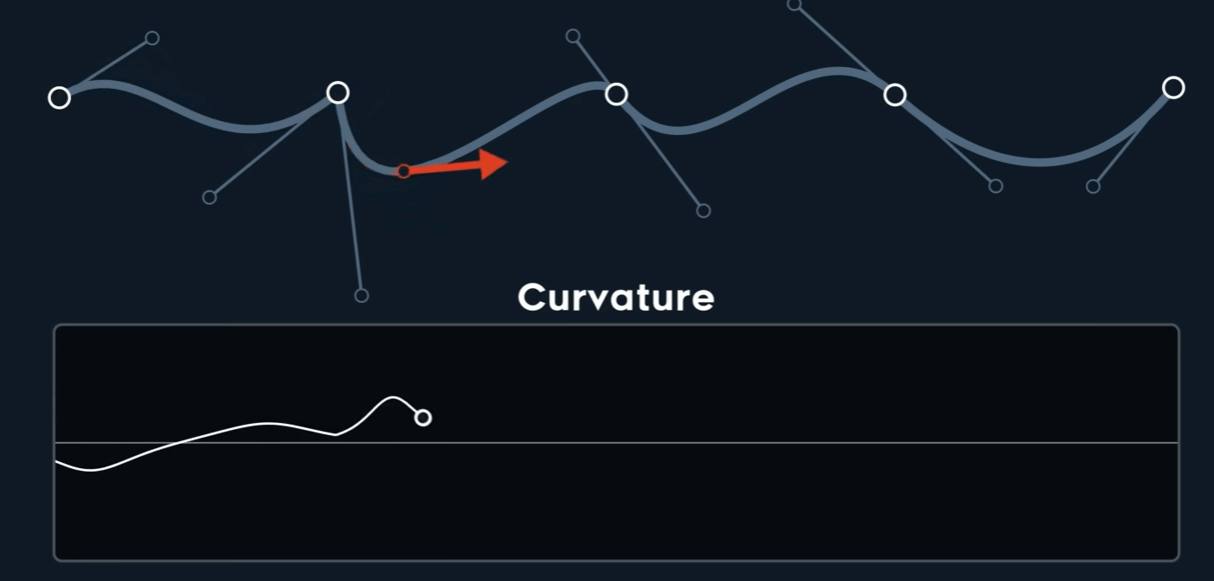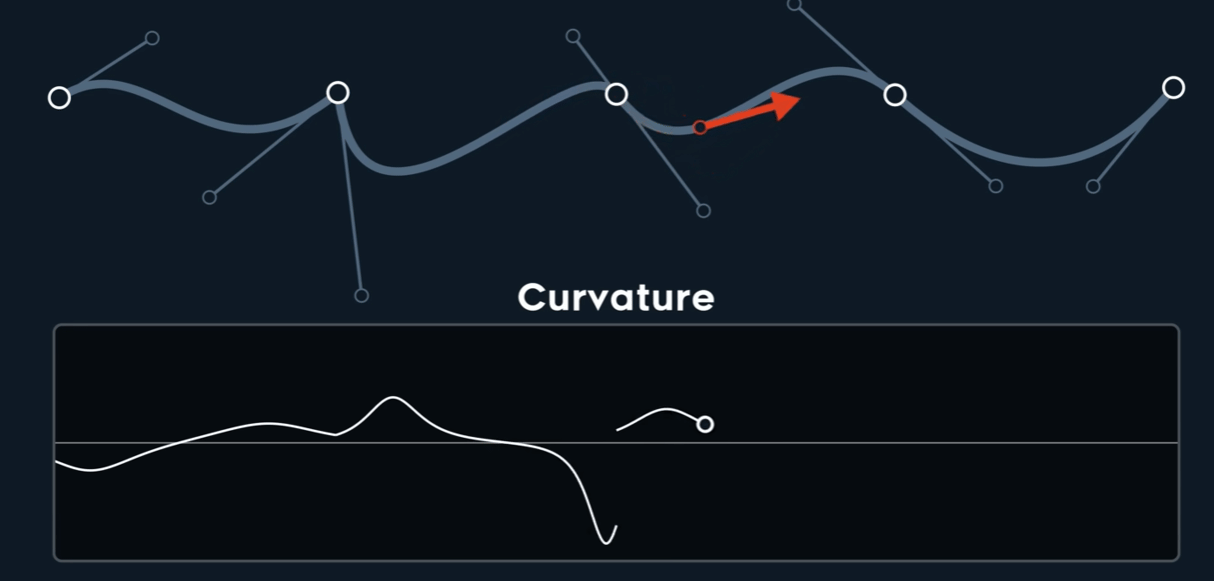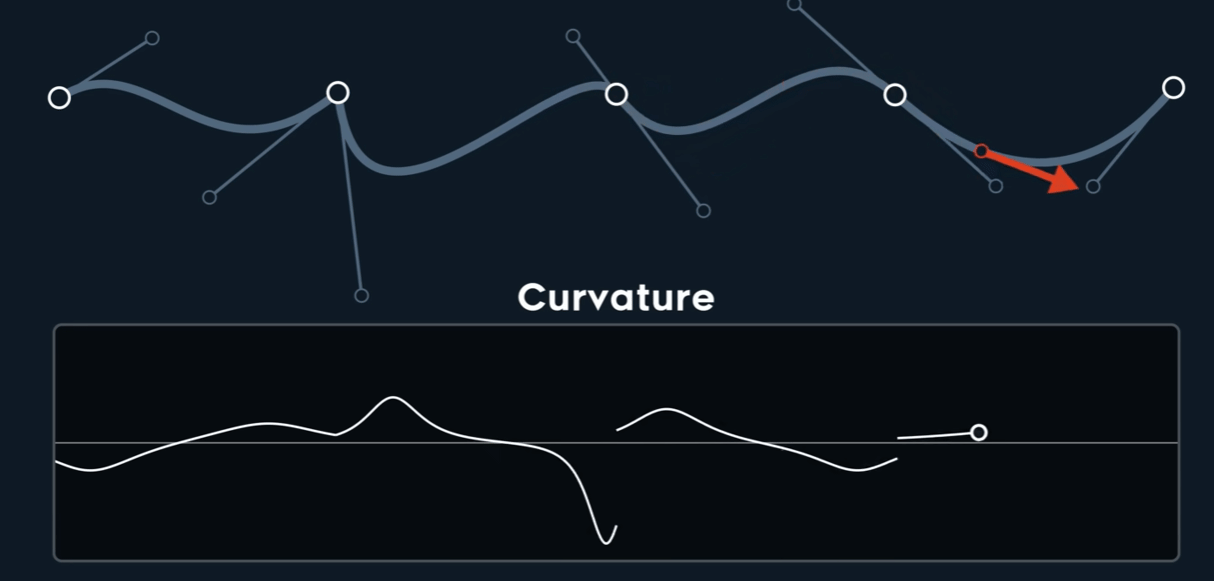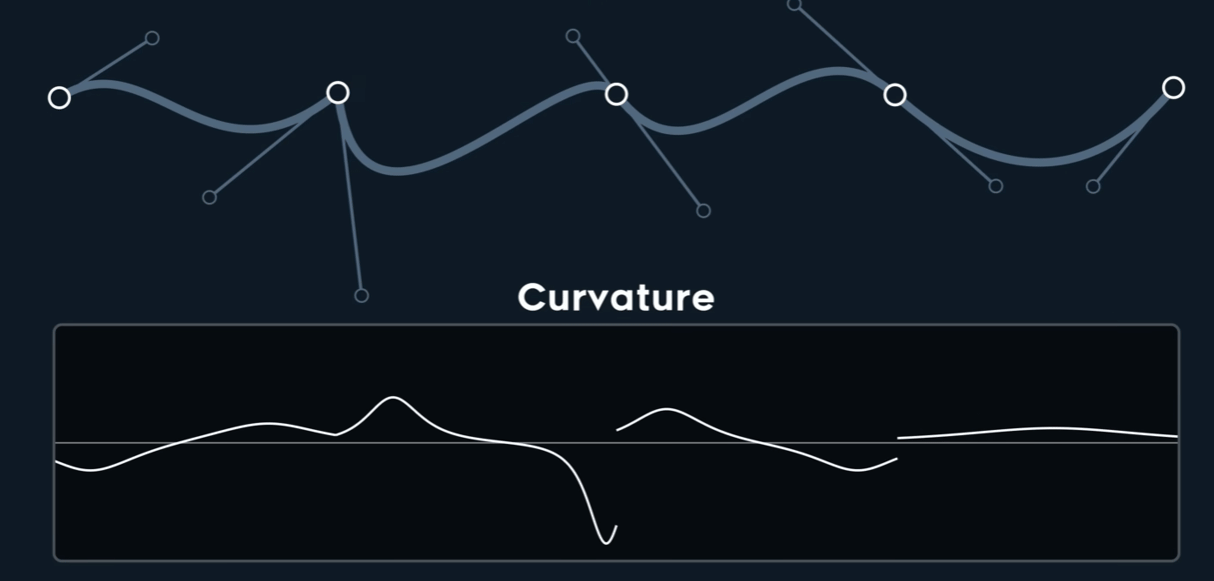
仅仅$C^{0}$时，也可能是Curvature连续的，而$C^{1}$时，未必连续。

$G^{2}$ 连续性

$$
\mathbf{P}_5 = \mathbf{P}_3 + (\mathbf{P}_3 - \mathbf{P}_2)(2\beta_1 + \beta_1^2 + \beta_2/2) + (\mathbf{P}_1 - \mathbf{P}_2)\beta_1^2
$$

$\mathbf{P}_5$ 被上述控制点与参数共同决定。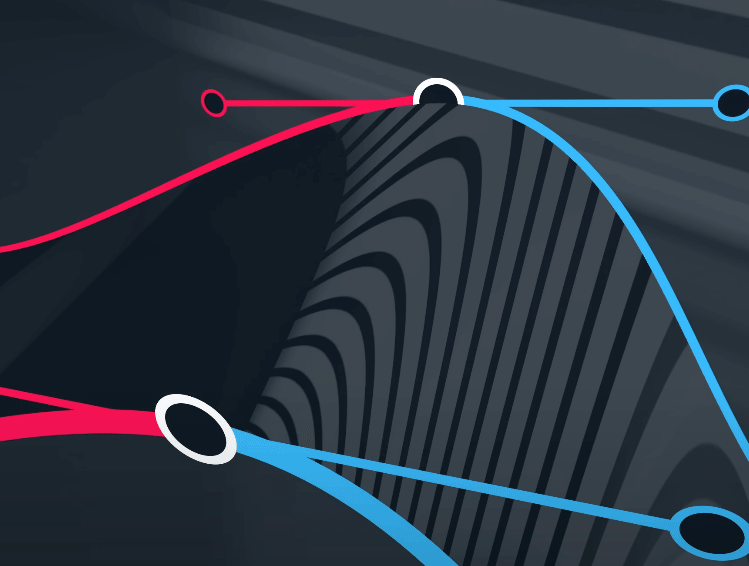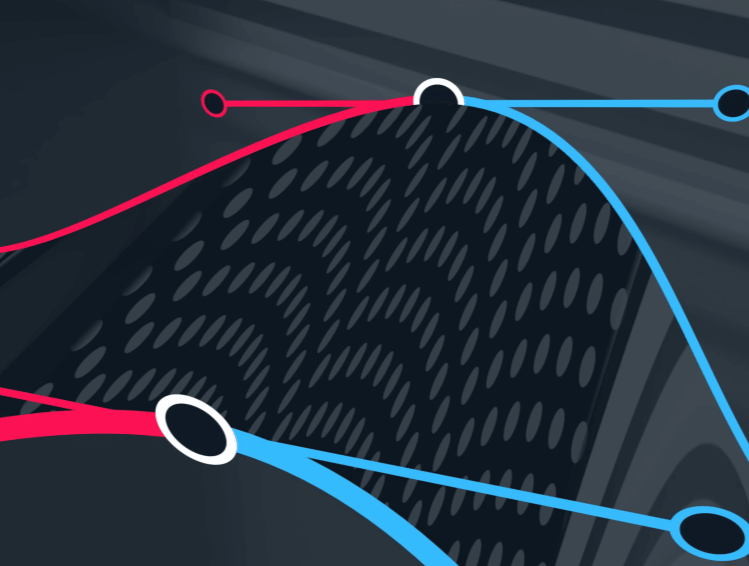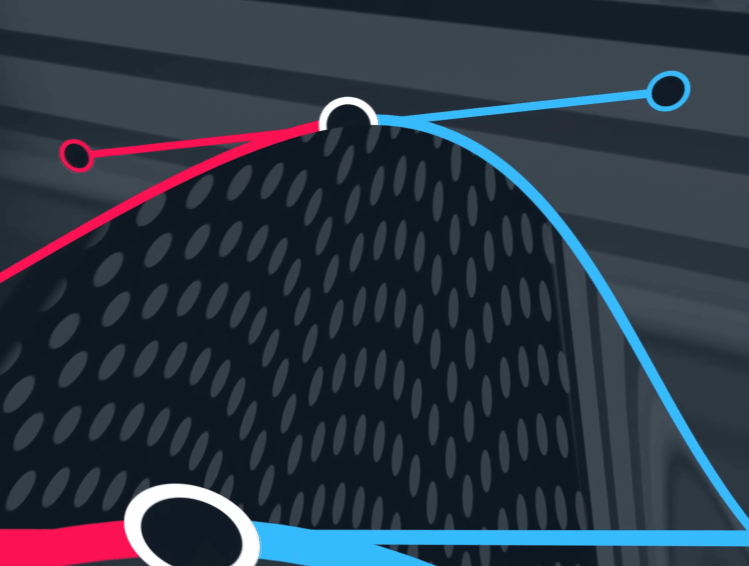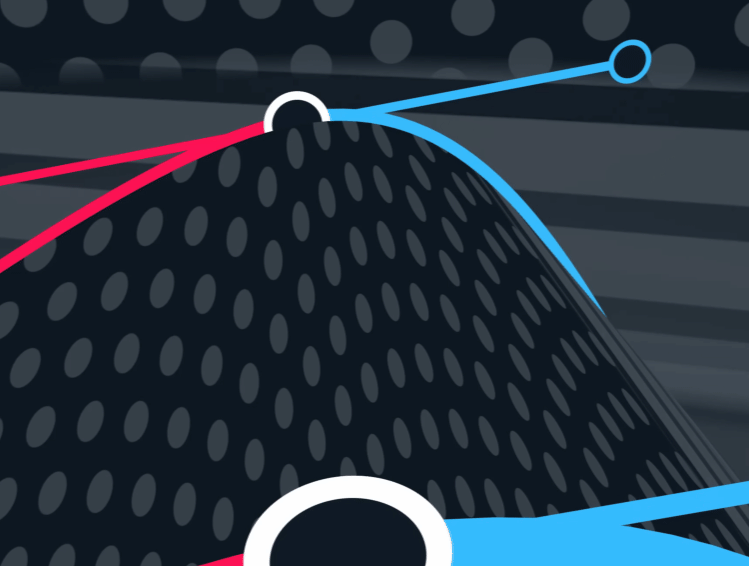

$G^{2}$ 以及以上被称为A级面

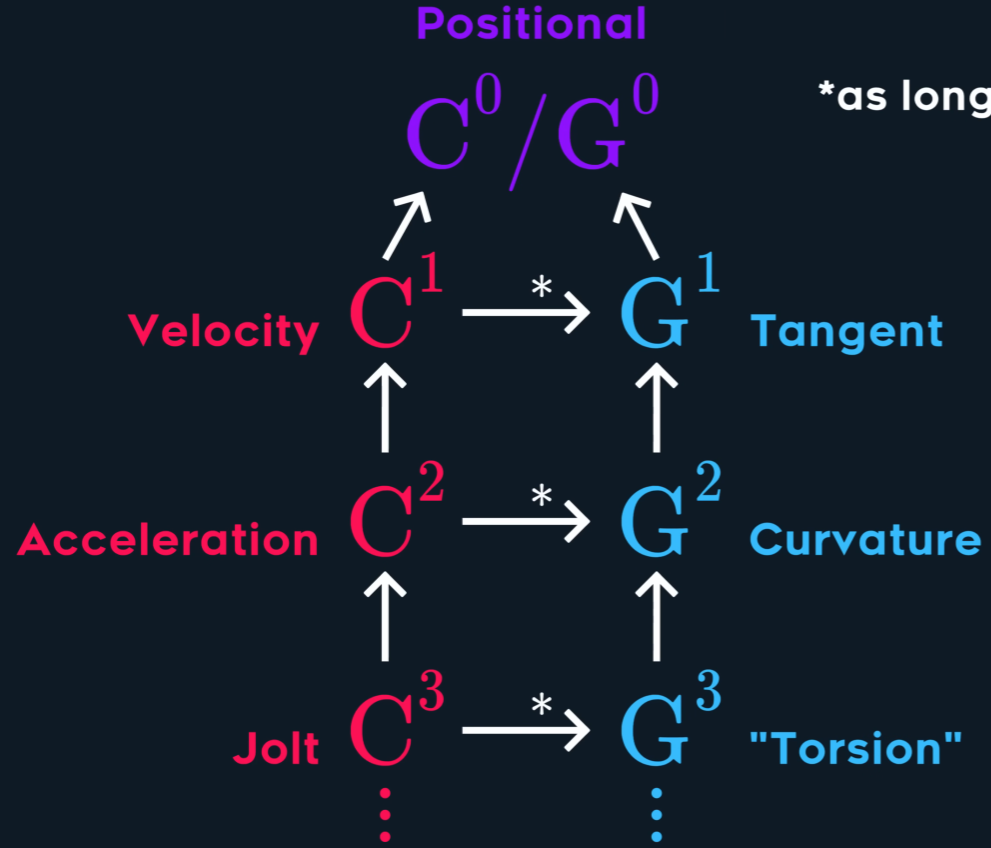
*as long as the curves are regular

Hermite Curves

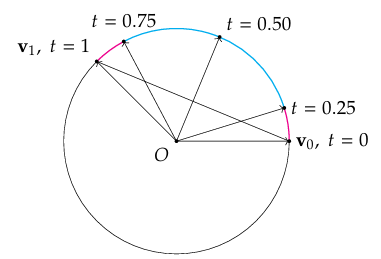
贝塞尔曲线利用四个控制点来构造，而Hermite曲线由两个端点和端点的速度。即
$$
P(0) = P_0 \\
P(1) = P_1 \\
P’(0) = \mathbf{v}_0 \\
P’(1) = \mathbf{v}_1
$$

通过上述关系求解
$$
P(t) = at^3 + bt^2 + ct + d
$$

得到
$$
\mathbf{P}(t) =
\begin{bmatrix}
1 & t & t^2 & t^3
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
-3 & -2 & 3 & -1 \\
2 & 1 & -2 & 1
\end{bmatrix}
\begin{bmatrix}
\mathbf{P}_0 \\
\mathbf{v}_0 \\
\mathbf{P}_1 \\
\mathbf{v}_1
\end{bmatrix}
$$

通过设置连接点处切向量相等，可以方便地实现$C^1$

Hermite to Bezier:
$$
B_0 = P_0 \\
B_1 = P_0 + v_0/3 \\
B_2 = P_1 - v_1/3 \\
B_3 = P_1
$$

Cardinal Spline

从此处开始$ \mathbf{P}_0$，$ \mathbf{P}_1$，$ \mathbf{P}_2$，$ \mathbf{P}_3$ 指的是spline上的相邻四个joints点

如何串联一系列给定的点呢？
我们可以采用一种类似Hermite的方法，我们计算一个joint相邻两点的位移，并以此作为此点的速度

但首尾两点并没有被穿进去，我们可以将原第二个点关于首个joint对称过去。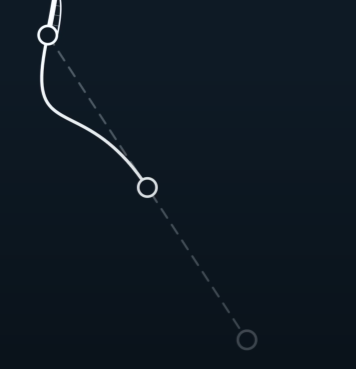

但是这样得到的曲线看起来有些呆板。出现了长段的较为平坦的线条，我们可以引入一个 Scale 参数 $s$ 来缩放我们的速度。当$s$接近于0的时候，也就退化成了线性spline

$$
\mathbf{P}(t) =
\begin{bmatrix}
1 & t & t^2 & t^3
\end{bmatrix}
\begin{bmatrix}
0 & 1 & 0 & 0 \\
-s & 0 & s & 0 \\
2s & s-3 & 3-2s & -s \\
-s & 2-s & s-2 & s
\end{bmatrix}
\begin{bmatrix}
\mathbf{P}_0 \\
\mathbf{P}_1 \\
\mathbf{P}_2 \\
\mathbf{P}_3
\end{bmatrix}
$$

当$s = 0.5$时，我们有

Catmull-Rom Spline

1. Interpolating every point!
2. $C^1$ continuous， not $C^{2}$
3. No need to specify tangents

$$
\mathbf{P}(t) = \begin{bmatrix} 1 & t & t^2 & t^3 \end{bmatrix} \frac{1}{2} \begin{bmatrix} 0 & 2 & 0 & 0 \\ -1 & 0 & 1 & 0 \\ 2 & -5 & 4 & -1 \\ -1 & 3 & -3 & 1 \end{bmatrix} \begin{bmatrix} \mathbf{P}_0 \\ \mathbf{P}_1 \\ \mathbf{P}_2 \\ \mathbf{P}_3 \end{bmatrix}
$$

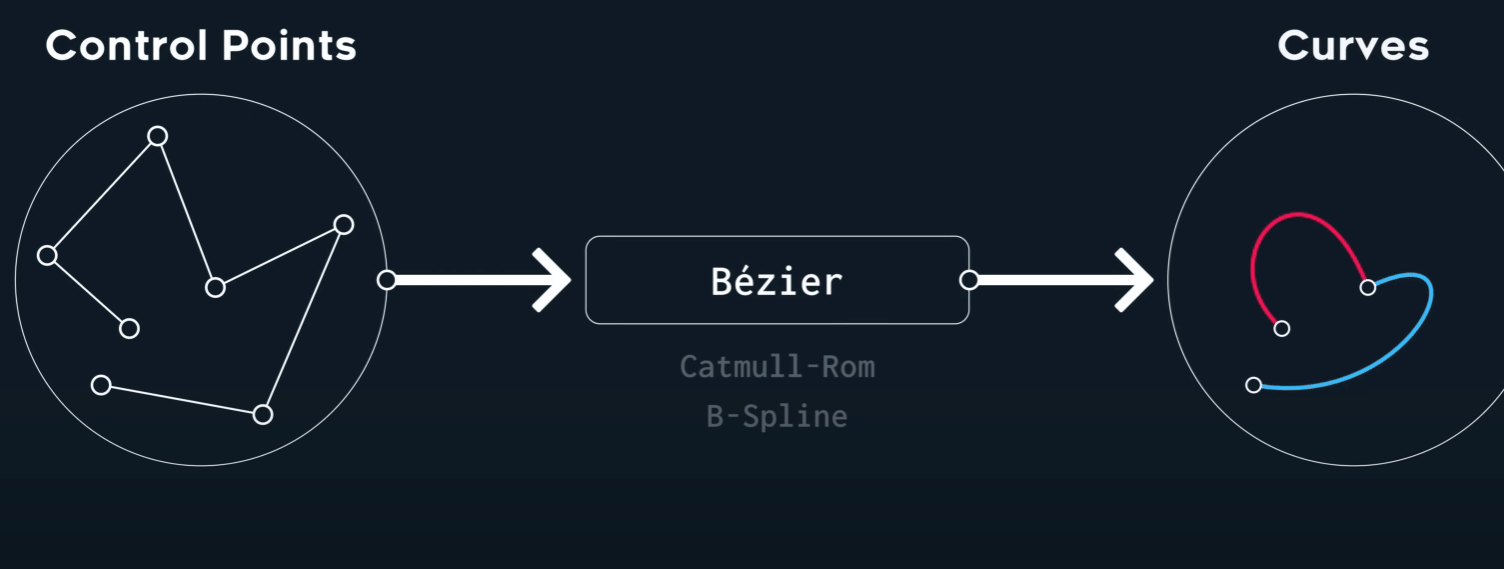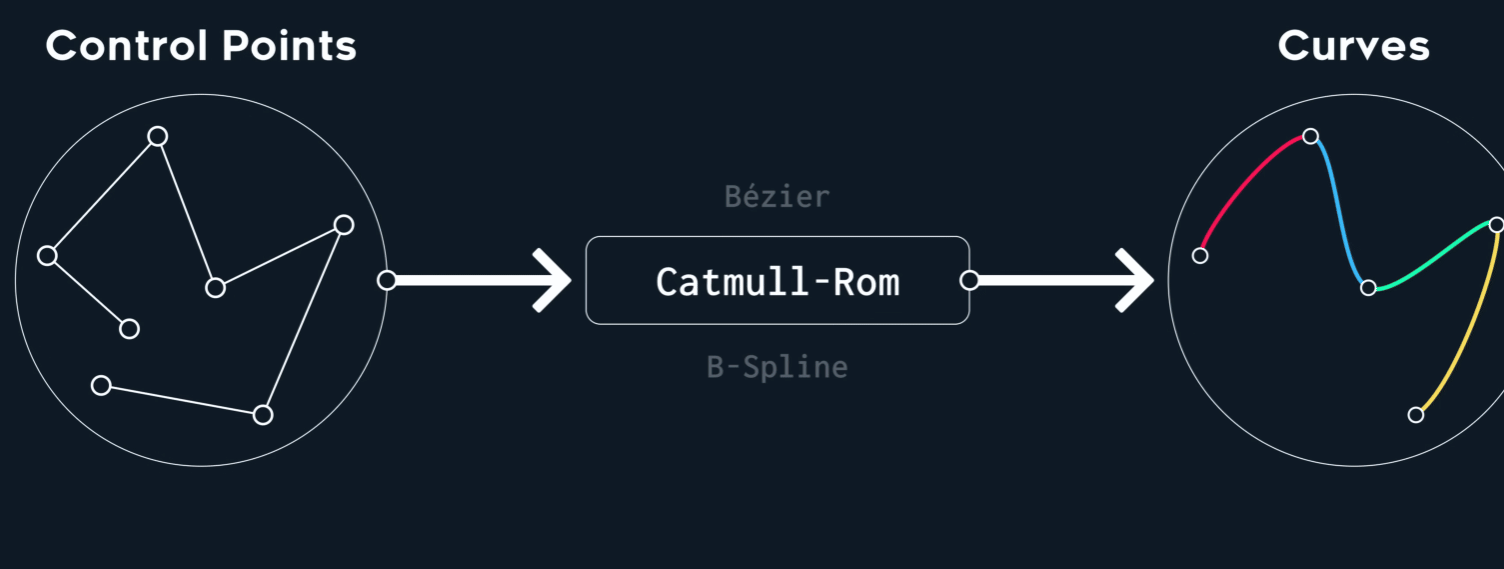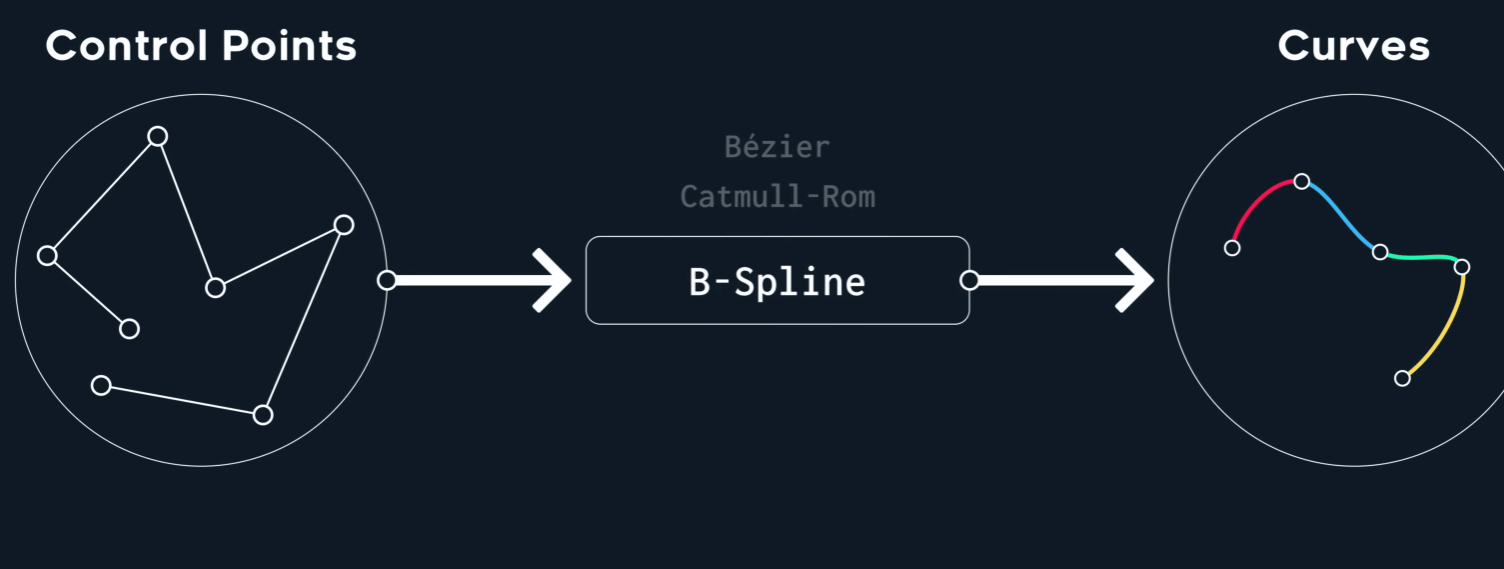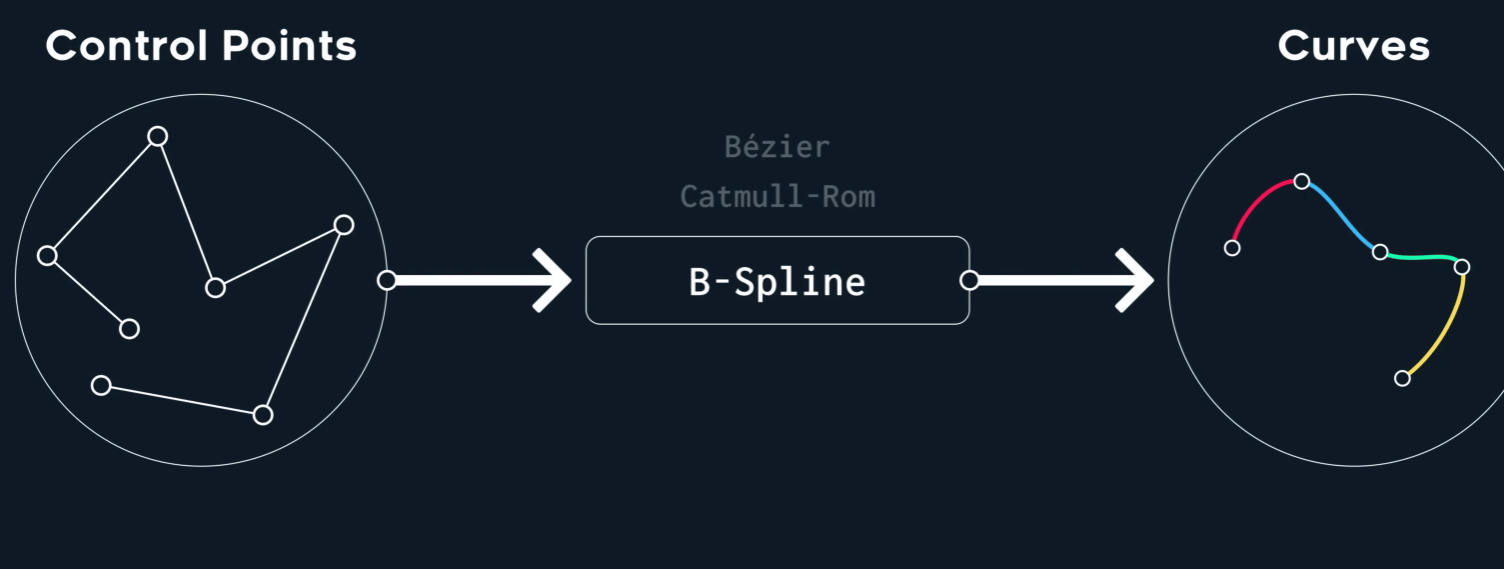
B-Spline(Basis-Spline)

那么，有没有一种构造Spline的方式，使之可以满足$C^2$呢？也就是说，我们要对这个求解：
$$
\mathbf{P}(t) =
\begin{bmatrix}
1 & t & t^2 & t^3
\end{bmatrix}
\begin{bmatrix}
\textcolor{red}{c_0} & \textcolor{cyan}{c_1} & \textcolor{green}{c_2} & \textcolor{orange}{c_3} \\
\textcolor{red}{c_4} & \textcolor{cyan}{c_5} & \textcolor{green}{c_6} & \textcolor{orange}{c_7} \\
\textcolor{red}{c_8} & \textcolor{cyan}{c_9} & \textcolor{green}{c_{10}} & \textcolor{orange}{c_{11}} \\
\textcolor{red}{c_{12}} & \textcolor{cyan}{c_{13}} & \textcolor{green}{c_{14}} & \textcolor{orange}{c_{15}}
\end{bmatrix}
\begin{bmatrix}
\textcolor{red}{\mathbf{P}_0} \\
\textcolor{cyan}{\mathbf{P}_1} \\
\textcolor{green}{\mathbf{P}_2} \\
\textcolor{orange}{\mathbf{P}_3}
\end{bmatrix}
$$

$$
\begin{gather}
\textcolor{red}{B_0(1) = 0} \tag{1} \
\textcolor{red}{B’{0}(1) = 0} \tag{2} \
\textcolor{red}{B’’{0}(1) = 0} \tag{3} \
\textcolor{red}{B_0(0)} = \textcolor{cyan}{B_1(1)} \tag{4} \
\textcolor{red}{B’{0}(0)} = \textcolor{cyan}{B’{1}(1)} \tag{5} \
\textcolor{red}{B’’{0}(0)} = \textcolor{cyan}{B’’{1}(1)} \tag{6} \
\textcolor{cyan}{B_1(0)} = \textcolor{green}{B_2(1)} \tag{7} \
\textcolor{cyan}{B’{1}(0)} = \textcolor{green}{B’{2}(1)} \tag{8} \
\textcolor{cyan}{B’’{1}(0)} = \textcolor{green}{B’’{2}(1)} \tag{9} \
\textcolor{green}{B_2(0)} = \textcolor{orange}{B_3(1)} \tag{10} \
\textcolor{green}{B’{2}(0)} = \textcolor{orange}{B’{3}(1)} \tag{11} \
\textcolor{green}{B’’{2}(0)} = \textcolor{orange}{B’’{3}(1)} \tag{12} \
\textcolor{orange}{B_3(0) = 0} \tag{13} \
\textcolor{orange}{B’{3}(0) = 0} \tag{14} \
\textcolor{orange}{B’’{3}(0) = 0} \tag{15} \
\textcolor{red}{B_0(t)} + \textcolor{cyan}{B_1(t)} + \textcolor{green}{B_2(t)} + \textcolor{orange}{B_3(t)} = 1 \tag{16}
\end{gather}
$$

$$
\mathbf{P}(t) =
\begin{bmatrix}
1 & t & t^2 & t^3
\end{bmatrix}
\frac{1}{6}
\begin{bmatrix}
1 & 4 & 1 & 0 \
-3 & 0 & 3 & 0 \
3 & -6 & 3 & 0 \
-1 & 3 & -3 & 1
\end{bmatrix}
\begin{bmatrix}
\textcolor{red}{\mathbf{P}_0} \
\textcolor{cyan}{\mathbf{P}_1} \
\textcolor{green}{\mathbf{P}_2} \
\textcolor{orange}{\mathbf{P}_3}
\end{bmatrix}
$$

• Not interpolating
• $C^2$ continuous! $G ^ 2$

B 样条的递推定义

refer to B样条的定义de boor-cox公式的理解

数学定义：
$$
P(t) = \sum_{i=0}^{n} P_i F_{i,k}(t) \qquad t \in [t_{k-1}, t_{n+1}]
$$

• $k$ 是 B 样条的次数

• $n$ 是控制点的最大索引，如果有$P_{i}, (i = 0, 1, …, n)$共 $n + 1$个控制点，那么最大索引就是$n$

• $i$ 是这些控制点的序号

de Boor-Cox 递推定义，只与 t 有关

基函数的递推：

$$
\left{
\begin{aligned}
& F_{i,0}(t) =
\begin{cases}
1, & t_i \le t < t_{i+1} \
0, & \text{其他}
\end{cases}
\[2ex]
& F_{i,k}(t) = \frac{t-t_i}{t_{i+k}-t_i} F_{i,k-1}(t) + \frac{t_{i+k+1}-t}{t_{i+k+1}-t_{i+1}} F_{i+1,k-1}(t)
\[2ex]
& \text{约定 } \frac{0}{0} = 0
\end{aligned}
\right.
$$

$i$ 是基函数的编号，每个$P_i$都有一个权重函数，也就是基函数。

$i$ 也是向量节点 $T$ 中节点的索引。基函数$F_{i,k}(t)$的具体形状，它在时间轴上的起点和终点，完全是由节点向量$T = [t_0, t_1, t_2, … ]$ 决定的。$i$ 告诉我们，基函数 $F_{i,k}(t)$ 在 $[t_i, t_{i+k+1}]$ 是不为零的。

控制点的递推：
$$
\begin{equation*}
\mathbf{P}{i,r}(t) = (1 - \alpha{i,r}) \mathbf{P}{i-1, r-1}(t) + \alpha{i,r} \mathbf{P}_{i, r-1}(t) \tag{}
\end{equation*}
$$

$$
\alpha_{i,r} = \frac{t - t_i}{t_{i+k+1-r} - t_i}
$$

$k$ 是 B 样条的次数，那么这个样条的阶数是$k+1$， 一段就有$k+1$个控制点

$r$ 是计算的轮数，$r$从1走到$k$

我们把所有的（不仅是某一段的）, 共(n + 1)个控制点记作 $P_{i}, (i = 0, 1, …, n)$ ，有 n + k +2 ($节点数 = 总控制点数 + 次数 + 1$) 个节点矢量 $T = [t_0, t_1, … t_{n + k + 1}]$

例如，5 个控制点，3次的B样条曲线，由于一段是由4个控制点决定的，那么就有（5-3 = ）2个线段，1个joint

对于零次B样条：

其基函数可以直接得到

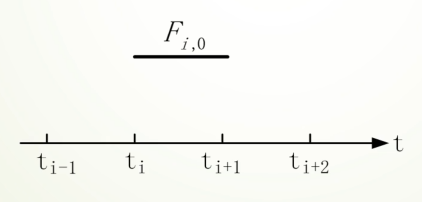
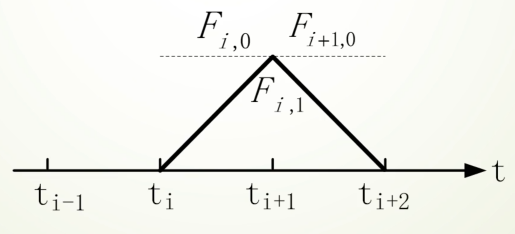
对于一次B样条：

$$
F_{i,1}(t) = \frac{t - t_i}{t_{i+1} - t_i} F_{i,0}(t) + \frac{t_{i+2} - t}{t_{i+2} - t_{i+1}} F_{i+1,0}(t)
$$

$$
F_{i+1,0}(t) =
\begin{cases}
1, & \text{若 } t_{i+1} \le t < t_{i+2} \[1.5ex]
0, & \text{其他}
\end{cases}
$$

对于二次 B 样条：

$$
F_{i,2}(t) = \frac{t-t_i}{t_{i+2}-t_i} F_{i,1}(t) + \frac{t_{i+3}-t}{t_{i+3}-t_{i+1}} F_{i+1,1}(t)
$$

$$
F_{i+1,1}(t) =
\begin{cases}
\frac{t-t_{i+1}}{t_{i+2}-t_{i+1}}, & \text{若 } t_{i+1} \le t < t_{i+2} \[2ex]
\frac{t_{i+3}-t}{t_{i+3}-t_{i+2}}, & \text{若 } t_{i+2} \le t < t_{i+3} \[2ex]
0, & \text{其他}
\end{cases}
$$

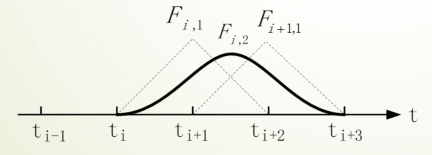
对于三次 B 样条：
$$
F_{i,3}(t) = \frac{t - t_i}{t_{i+3} - t_i} F_{i,2}(t) + \frac{t_{i+4} - t}{t_{i+4} - t_{i+1}} F_{i+1,2}(t)
$$

$$
F_{i+1,2}(t) =
\begin{cases}
\frac{t - t_{i+1}}{t_{i+3} - t_{i+1}} \cdot \frac{t - t_{i+1}}{t_{i+2} - t_{i+1}}, & \text{若 } t_{i+1} \le t < t_{i+2} \[3ex]
\frac{t-t_{i+1}}{t_{i+3}-t_{i+1}} \cdot \frac{t_{i+3}-t}{t_{i+3}-t_{i+2}} + \frac{t_{i+4}-t}{t_{i+4}-t_{i+2}} \cdot \frac{t-t_{i+2}}{t_{i+3}-t_{i+2}}, & \text{若 } t_{i+2} \le t < t_{i+3} \[3ex]
\frac{(t_{i+4}-t)^2}{(t_{i+4}-t_{i+2})(t_{i+4}-t_{i+3})}, & \text{若 } t_{i+3} \le t < t_{i+4} \[3ex]
0, & \text{其他}
\end{cases}
$$

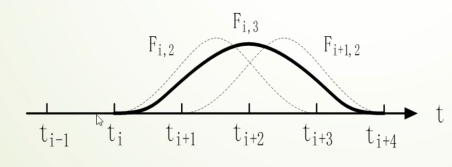
例

三次 B 样条, 控制点为$P_0 = (30, 0)$, $P_1 = (60, 10)$, $P_2 = (80, 30)$, $P_3 = (90, 60)$, $P_4 = (90, 90)$，节点向量(Knot Vector): $T = [t_0, t_1, t_2, t_3,t_4,t_5,t_6,t_7, t_8] = [0,0,0,0,0.5, 1,1,1,1]$
求曲线上一点 $P(\frac{1}{4})$ 的值

首先观察这个点在哪个区间上，由于$t_3 = 0 < \frac{1}{4} < t_4 = 0.5$， 那么这个区间的索引是 $i = 3$

在区间$[t_i, t_{i+1})$内， 对于$k$次B样条，需要用到$k + 1$个控制点，这些点的索引是$P_{i-k}$, $P_{i-k +1}, … P_{i}$

那么，在区间$[t_3, t_{4})$ 内，对于3次B样条，需要用到4个控制点，这些点的索引是$P_0, P_1, P_2, P_3$

对于 k 次B样条，需要经行 k 轮运算，每一轮都使用上一轮计算出的点进行插值。

回顾数学定义：
$$
P(t) = \sum_{i=0}^{n} P_i F_{i,k}(t)
$$

$$
P(\frac{1}{4}) = \sum_{i=0}^{3} P_i F_{i,3}(\frac{1}{4}) \
P(\frac{1}{4}) = P_0F_{0,3}(\frac{1}{4}) + P_1 F_{1,3}(\frac{1}{4}) + P_2 F_{2,3}(\frac{1}{4}) + P_3F_{3,3}(\frac{1}{4})
$$

据此，利用上述的关于$F_{i,k}$的递推关系，我们可以算出各个$F_{i,k}$ 的值，进而$P(\frac{1}{4})$的值。不过，基于$F_{i,k}$的递推关系，我们可以找到一些最终值和控制点的关系：
$$
\begin{equation*}
\mathbf{P}{i,r}(t) = (1 - \alpha{i,r}) \mathbf{P}{i-1, r-1}(t) + \alpha{i,r} \mathbf{P}_{i, r-1}(t) \tag{}
\end{equation*}
$$

$$
\alpha_{i,r} = \frac{t - t_i}{t_{i+k+1-r} - t_i}
$$

第一轮计算，也就是 $r = 1$：

计算 $P_{1,1}$ ，由 $P_{0,0}$ 和 $P_{1,0}$ 插值得到

• 权重 $
  \alpha_{1,1} = \frac{t - t_1}{t_{1+3+1-1} - t_1} = \frac{0.25 - t_1}{t_4 - t_1} = \frac{0.25 - 0}{0.5 - 0} = 0.5
  $

• $P_{1,1} = (1 - 0.5)P_{0,0} + 0.5 \cdot P_{1,0} = 0.5(30,0) + 0.5(60,10) = (15,0) + (30,5) = (45, 5)$

计算 $P_{2,1}$ (由 $P_{1,0}$ 和 $P_{2,0}$ 插值得到):

• 权重 $\alpha_{2,1} = \frac{t - t_2}{t_{2+3+1-1} - t_2} = \frac{0.25 - t_2}{t_5 - t_2} = \frac{0.25 - 0}{1 - 0} = 0.25$
• $P_{2,1} = (1 - 0.25)P_{1,0} + 0.25 \cdot P_{2,0} = 0.75(60,10) + 0.25(80,30) = (45, 7.5) + (20, 7.5) = (65, 15)$

计算 $P_{3,1}$ (由 $P_{2,0}$ 和 $P_{3,0}$ 插值得到):

• 权重 $\alpha_{3,1} = \frac{t - t_3}{t_{3+3+1-1} - t_3} = \frac{0.25 - t_3}{t_6 - t_3} = \frac{0.25 - 0}{1 - 0} = 0.25$
• $P_{3,1} = (1 - 0.25)P_{2,0} + 0.25 \cdot P_{3,0} = 0.75(80,30) + 0.25(90,60) = (60, 22.5) + (22.5, 15) = (82.5, 37.5)$

第二轮计算，也就是 $r = 2$：
计算 $P_{2,2}$ (由 $P_{1,1}$ 和 $P_{2,1}$ 插值得到):
权重 $\alpha_{2,2} = \frac{t - t_2}{t_{2+3+1-2} - t_2} = \frac{0.25 - t_2}{t_4 - t_2} = \frac{0.25 - 0}{0.5 - 0} = 0.5$
$P_{2,2} = (1 - 0.5)P_{1,1} + 0.5 \cdot P_{2,1} = 0.5(45,5) + 0.5(65,15) = (22.5, 2.5) + (32.5, 7.5) = (55, 10)$

计算 $P_{3,2}$ (由 $P_{2,1}$ 和 $P_{3,1}$ 插值得到):
权重 $\alpha_{3,2} = \frac{t - t_3}{t_{3+3+1-2} - t_3} = \frac{0.25 - t_3}{t_5 - t_3} = \frac{0.25 - 0}{1 - 0} = 0.25$
$P_{3,2} = (1 - 0.25)P_{2,1} + 0.25 \cdot P_{3,1} = 0.75(65,15) + 0.25(82.5, 37.5) = (48.75, 11.25) + (20.625, 9.375) = (69.375, 20.625)$

第三轮计算 ($r = 3$)，最终结果
计算 $P_{3,3}$ (由 $P_{2,2}$ 和 $P_{3,2}$ 插值得到):
权重 $\alpha_{3,3} = \frac{t - t_3}{t_{3+3+1-3} - t_3} = \frac{0.25 - t_3}{t_4 - t_3} = \frac{0.25 - 0}{0.5 - 0} = 0.5$
$P_{3,3} = (1 - 0.5)P_{2,2} + 0.5 \cdot P_{3,2} = 0.5(55,10) + 0.5(69.375, 20.625)$
$P_{3,3} = (27.5, 5) + (34.6875, 10.3125) = (62.1875, 15.3125)$

Trajectory

$$
\begin{bmatrix} 1 & 0 & 0 & 0 \ 0 & 1! & 0 & 0 \ 0 & 0 & 1/2! & 0 \ 0 & 0 & 0 & 1/3! \end{bmatrix} \begin{bmatrix} \mathbf{p}_0 \ \mathbf{v}_0 \ \mathbf{g}_0 \ \mathbf{j}_0 \end{bmatrix}
$$

$$
\mathbf{P}(t) = \begin{bmatrix} 1 & t & t^2 & t^3 \end{bmatrix} \begin{bmatrix} \mathbf{p}_0 \ \mathbf{v}_0 \ \frac{1}{2}\mathbf{g}_0 \ \frac{1}{6}\mathbf{j}_0 \end{bmatrix} = \mathbf{p}_0 \cdot 1 + \mathbf{v}_0 \cdot t + \left(\frac{1}{2}\mathbf{g}_0\right) \cdot t^2 + \left(\frac{1}{6}\mathbf{j}_0\right) \cdot t^3
$$

Conclusion

Handling Non-Uniform Time in Splines

目前讨论的是最经典的情况，即每个曲线段的“时长”都是1个单位（称之为**参数化均匀 (Uniform Parameterization)**）。

当每个曲线段的实际时间或“长度”不同时（参数化非均匀, Non-Uniform Parameterization），我们需要对连续性的定义进行一些调整。核心思想是：我们关心的连续性（如速度、加速度）是相对于真实时间 T 的，而不是曲线的局部参数 u 的。

1. 核心变化：全局时间 (T) vs 局部参数 (u)

首先，我们要区分两个概念：

• 局部参数 u：这始终是从0到1变化的值，用来在单个贝塞尔曲线段内部进行插值。你的笔记中所有的 f(u) 都是基于此。
• **全局时间 T**：这是整个样条的“真实”时间轴。

假设第 i 段曲线的开始时间是 Tᵢ，结束时间是 Tᵢ₊₁。那么该段的持续时间是 ΔTᵢ = Tᵢ₊₁ - Tᵢ。
我们可以将全局时间 T 转换为该段的局部参数 u：
$$u = \frac{T - T_i}{T_{i+1} - T_i} = \frac{T - T_i}{\Delta T_i}$$

2. 关键：使用链式法则 (Chain Rule) 重新定义连续性

物理上的速度和加速度是曲线 P 对全局时间 T 的导数，而不是对 u 的导数。我们需要使用链式法则来连接它们：

一阶导数 (速度)

$$\frac{dP}{dT} = \frac{dP}{du} \cdot \frac{du}{dT}$$
从上面的公式我们知道 du/dT = 1 / ΔTᵢ。所以：
$$\mathbf{P}’(T) = \frac{1}{\Delta T_i} \mathbf{P}’(u)$$
这意味着，真实的速度向量是 P'(u) 的一个缩放版本，缩放因子是该段时间间隔的倒数。

二阶导数 (加速度)

对一阶导数再次求导：
$$
\frac{d^2P}{dT^2} = \frac{d}{dT}\left( \frac{1}{\Delta T_i} \frac{dP}{du} \right) = \frac{1}{\Delta T_i} \cdot \frac{d}{dT}\left(\frac{dP}{du}\right)
$$

再次使用链式法则：

$$
\mathbf{P}’’(T) = \frac{1}{\Delta T_i} \cdot \frac{d}{du}\left(\frac{dP}{du}\right) \cdot \frac{du}{dT} = \frac{1}{\Delta T_i} \cdot \mathbf{P}’’(u) \cdot \frac{1}{\Delta T_i} = \frac{1}{(\Delta T_i)^2} \mathbf{P}’’(u)
$$
真实加速度的缩放因子是时间间隔平方的倒数。

3. 如何修正上述的Splines？

现在我们把这个理论应用到样条上。

A. 贝塞尔曲线的 $C^1$ 连续性

为了实现 $C^1$ 连续，需要满足 b₄ = 2b₃ - b₂，这意味着控制点 b₃ 是 b₂ 和 b₄ 的中点（所谓的 “Mirror”）。这是因为我们假设了两段曲线的 ΔT 相同，所以我们让 P'(u) 在连接点处相等。

在非均匀时间下，我们需要让真实速度 P'(T) 相等。

• 第一段曲线（控制点 $b_0, b_1, b_2, b_3$，时长 $\Delta T_0$）在连接点 $b_3$ 的速度是：
  $$\mathbf{P}’(T_1) = \frac{1}{\Delta T_0} \mathbf{P}’(u=1) = \frac{3}{\Delta T_0} (b_3 - b_2)$$
• 第二段曲线（控制点 $b_3, b_4, b_5, b_6$，时长 $\Delta T_1$）在连接点 $b_3$ 的速度是：
  $$\mathbf{P}’(T_1) = \frac{1}{\Delta T_1} \mathbf{P}’(u=0) = \frac{3}{\Delta T_1} (b_4 - b_3)$$

让它们相等：
$$
\frac{3}{\Delta T_0} (b_3 - b_2) = \frac{3}{\Delta T_1} (b_4 - b_3)
$$
整理后得到：
$$
\frac{b_3 - b_2}{\Delta T_0} = \frac{b_4 - b_3}{\Delta T_1}
$$
结论：控制点 b₂, b₃, b₄ 仍然需要共线，但 b₃ 不再是中点。b₃ 到 b₂ 和 b₄ 的距离之比等于两段曲线的时间长度之比：
$$
\frac{\vert \vert b_3 - b_2 \vert \vert}{\vert \vert b_4 - b_3 \vert \vert} = \frac{\Delta T_0}{\Delta T_1}
$$

“Mirror” 关系变成了一个按时间比例缩放的“加权”关系。

均匀情况下的 Catmull-Rom

Catmull-Rom 的核心是它能自动计算每个点 Pᵢ 上的切线向量 vᵢ，计算方法是：
$$\mathbf{v}i = \frac{1}{2} (\mathbf{P}{i+1} - \mathbf{P}_{i-1})$$
这个公式的本质是一个几何上的平均。它假设从 Pᵢ₋₁ 到 Pᵢ 和从 Pᵢ 到 Pᵢ₊₁ 所花费的“时间”或“代价”是相同的，所以它给予了前后两个点完全相等的权重。

问题：为什么在非均匀时间下会失效？

想象一下这三个点在时间轴上的位置：

• Pᵢ₋₁ 在 T = 0
• Pᵢ 在 T = 1
• Pᵢ₊₁ 在 T = 10

从 Pᵢ₋₁ 到 Pᵢ 只花了1秒，而从 Pᵢ 到 Pᵢ₊₁ 花了9秒。显然，Pᵢ 点的瞬时速度应该更接近于前一段的“高速”状态，而不是被后一段“慢速”状态平均掉。均匀公式 vᵢ = 0.5 * (Pᵢ₊₁ - Pᵢ₋₁) 完全忽略了时间信息，会导致计算出的切线不符合物理直觉。

解决方案：基于“弦速度”的加权平均

为了解决这个问题，我们需要将切线的计算从几何向量升级为物理速度。

1. 计算弦速度 (Chord Velocity)
   我们把连接相邻两个点的直线段称为“弦”。我们可以计算出每根弦的平均速度。

   • Pᵢ 前一根弦的平均速度: $\mathbf{S}{i-1} = \frac{\mathbf{P}i - \mathbf{P}{i-1}}{T_i - T{i-1}} = \frac{\mathbf{P}i - \mathbf{P}{i-1}}{\Delta T_{i-1}}$
   • Pᵢ 后一根弦的平均速度: $\mathbf{S}{i} = \frac{\mathbf{P}{i+1} - \mathbf{P}i}{T{i+1} - T_i} = \frac{\mathbf{P}_{i+1} - \mathbf{P}i}{\Delta T{i}}$

2. 平均弦速度得到切线
   最直接的非均匀 Catmull-Rom 实现，就是将这两个物理意义上的弦速度进行平均，以此作为 Pᵢ 点的切线：
   $$\mathbf{v}i = \frac{1}{2} (\mathbf{S}{i-1} + \mathbf{S}{i}) = \frac{1}{2} \left( \frac{\mathbf{P}i - \mathbf{P}{i-1}}{\Delta T{i-1}} + \frac{\mathbf{P}_{i+1} - \mathbf{P}i}{\Delta T{i}} \right)$$
   这个公式现在包含了时间间隔 ΔT，使得时间短（速度快）的线段对切线方向和大小的贡献更大，这远比均匀版本要合理。

均匀情况下的 B-Spline

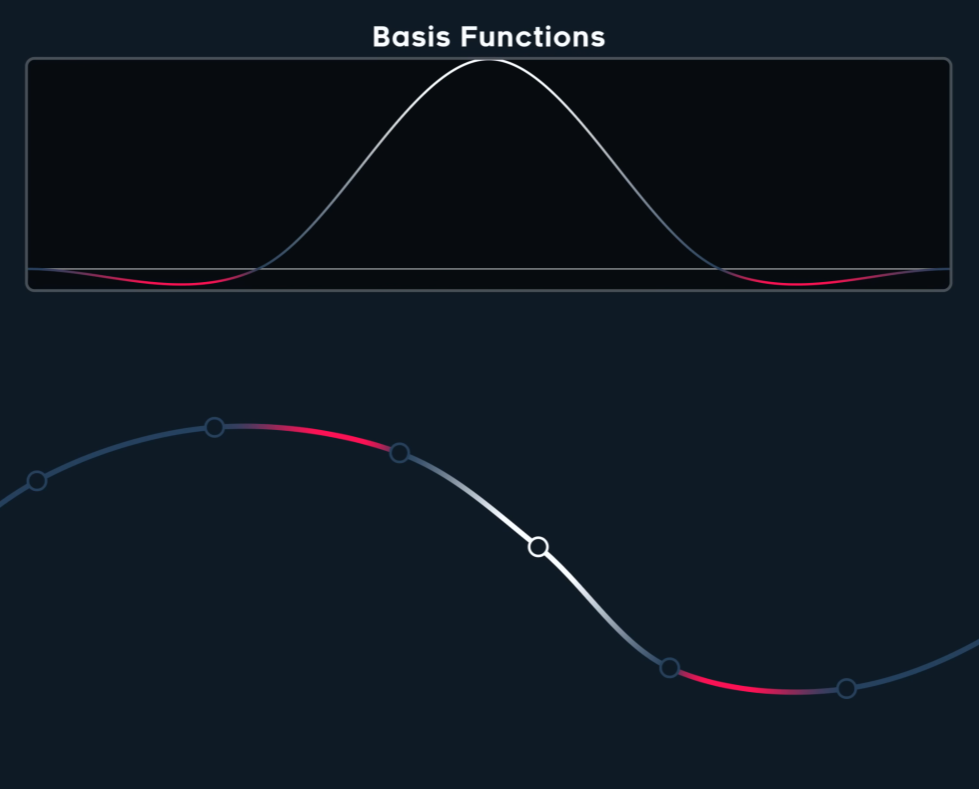
均匀 B-Spline 的节点向量是等距的，例如 [0, 1, 2, 3, 4, 5, ...]。这导致：

• 所有基函数（Basis Functions）B(t) 的形状都是完全一样的，只是在时间轴上进行了平移。
• 曲线的行为在任何地方都是一致的，控制点的移动对曲线形状的影响也是可预测且均匀的。

2. 解决方案：非均匀节点向量 (Non-Uniform Knot Vector)

非均匀 B-Spline 允许节点向量中的值不均匀分布，例如 [0, 0, 0, 1.5, 3.2, 5.0, 5.0, 5.0]。这个看似简单的改变带来了巨大的灵活性。

1. 改变基函数的形状
   B-Spline 的基函数是通过 Cox-de Boor 递归公式定义的。我们来看看这个公式（以k次样条为例）：
   $$B_{i,k}(t) = \frac{t - t_i}{t_{i+k} - t_i} B_{i,k-1}(t) + \frac{t_{i+k+1} - t}{t_{i+k+1} - t_{i+1}} B_{i+1,k-1}(t)$$
   请注意分母中的 tᵢ₊ₖ - tᵢ。这些项是节点向量中不同节点值之间的差。

   • 在均匀情况下，这些差值总是相同的。
   • 在非均匀情况下，这些差值是变化的！这意味着基函数的形状本身会根据节点间距的不同而改变。如果节点靠得很近，对应的基函数会变得又高又窄；如果节点分得很开，基函数会变得又矮又宽。

2. 控制曲线的局部行为
   由于基函数的形状可以改变，我们可以通过操纵节点向量来精确控制曲线的行为：

   • 改变速度：将一段区域内的节点排得更紧密，会使曲线在这段“时间”内更快地变化，因为它要更快地经过受这些节点影响的控制点。
   • 改变连续性：这是非均匀B-Spline最强大的特性之一。在一个节点上重复多次（增加节点的“重数”，Multiplicity），可以降低该点的连续性。对于三次B-Spline（通常是 $C^2$ 连续）：
     • 无重复节点 (重数为1): $C^2$ 连续 (曲率连续)。
     • 重复1次 (重数为2): 降为 $C^1$ 连续 (切线连续，但曲率不连续，可形成平滑拐角)。
     • 重复2次 (重数为3): 降为 $C^0$ 连续 (位置连续，但切线不连续，可形成尖角)。
     • 重复3次 (重数为4，即k+1次): 曲线会穿过对应的控制点。

总结：B-Spline 通过其核心定义——非均匀节点向量——来原生处理非均匀参数化。

总结

Refer to: quaternion.pdf quaternion by Krasjet

坐标系

本文将使用右手坐标系统， 用右手定则来定义旋转的正方向，即右手拇指指向旋转轴的 $\bf{u}$ 的正方向，这时其它 四个手指弯曲的方向即为旋转的正方向。

基础

• 点乘，标量积

可以看到，$\boldsymbol{v}_{||}$其实就是 $\boldsymbol{v}$ 在 $\boldsymbol{u}$ 上的正交投影(OrthogonalProjection)，根据 正交投影的公式，我们可以得出：

我们需要处理正交于 $\boldsymbol{u}$ 的 $\bf v_{\perp}$

方向永远垂直于矢量ab所在的平面啊。具体方向由右手定则决定。四指跟从向量A和B的旋转方向时，大拇指所朝的方向。

对于四元数 $q = a + bi +cj + dk$， $i^{2} = j^{2} = k^{2} = ijk = -1$

逆和共轭

$q^{-1}$是$q$的逆，规定：
$$
qq^{-1} = q^{-1} q = 1 (q \neq 0)
$$
有
$$
(pq)q^{-1} = p(qq^{-1}) = p \cdot 1 = p \
q^{-1}(qp) = (q^{-1}q)p = 1 \cdot p = p
$$

如果 $|| q || = 1$， 也就是说 $q$ 是一个单位四元数，那么
$$
q^{-1} = \frac{q ^*}{1^{2}} = q^* = [s, \bf{-v}]
$$

旋转

换言之，当我们有 $q= [\cos(\theta), \sin(\theta)\bf{u}]$时，那么$v’ = qvq^*$ 可以将 $\bf{v}$ 沿着 $\bf{u}$ 旋转 2$\theta$ 度。

我们把 $\bf{v}$ 写作一个纯四元数，然后按照四元数乘法进行运算，注意，四元数乘法有结合律，但四元数乘法通常没有交换律。

左乘一个四元数 $q = a + bi +cj + dk$ 等同于左乘下面这个矩阵：
$$
L(q) = \begin{bmatrix}
a & -b & -c & -d \\
b & a & -d & c \\
c & d & a & -b \\
d & -c & b & a
\end{bmatrix}
$$

右乘 $q$ 等同于这个左乘这个矩阵：
$$
R(q) = \begin{bmatrix}
a & -b & -c & -d \\
b & a & d & -c \\
c & -d & a & b \\
d & c & -b & a
\end{bmatrix}
$$

我们有：$qvq^* = L(q)R(q^*)v = R(q^*)L(q)v$, 注意$R(q^*) = R(q)^{T}$

也就是：
$$
qvq^* = \begin{bmatrix}
1 & 0 & 0 & 0 \
0 & 1 - 2c^2 - 2d^2{} & 2bc - 2ad & 2ac + 2bd \
0 & 2bc + 2ad & 1 - 2b^2 - 2d^2 & 2cd - 2ab \
0 & 2bd - 2ac & 2ab + 2cd & 1 - 2b^2 - 2c^2
\end{bmatrix} v
$$

四元数， 轴-角， 旋转矩阵， 欧拉角转换

任意向量 $\bf{v}$ 沿着以单位向量定义的旋转轴 $\bf{u}$ 旋转 $\theta$ 角度之后的 $\bf{v’}$ 可以使用矩阵乘法来获得。

令 $v = [0, \boldsymbol{v} ], q = [\cos(\frac{\theta}{2}), \sin(\frac{\theta}{2})\boldsymbol{u}]$

四元数与3D旋转的关系并不是一对一的，同一个3D旋转可以使用两个不同的四元数来表示。
对于任意的$q = [\cos(\frac{\theta}{2}), \sin(\frac{\theta}{2})\boldsymbol{u}]$，$q$与$-q$ 代表的是同一个旋转。如果𝑞表示的是沿着旋转轴$\bf{u}$旋转θ度，那么−𝑞代表的是沿着相反的旋转轴$- \bf{u}$旋转(2𝜋−θ)度。

对于常见的 ZYX 顺序（Unity Inspector 中使用的顺序，对应先绕Y轴，再绕X轴，再绕Z轴应用旋转，或者说物体先绕自身的Z轴，再绕自身新的X轴，再绕自身新的Y轴）： $q_X=[cos(α/2),sin(α/2)(1,0,0)]$ $q_Y=[cos(β/2),sin(β/2)(0,1,0)]$ $q_Z=[cos(γ/2),sin(γ/2)(0,0,1)]$ 最终的四元数 $q=q_Y⋅q_X⋅q_Z$ (注意乘法顺序，取决于欧拉角的具体定义是内旋还是外旋，以及轴的顺序)。

这个转换是明确的：给定一组特定顺序的欧拉角，总能计算出唯一的一个四元数（不考虑 q 和 −q 的等价性）。

插值

假设有两个旋转变换 $q_0 = [\cos(\frac{\theta_0}{2}), \sin(\frac{\theta_0}{2})\boldsymbol{u_0}]$, $q_1 = [\cos(\frac{\theta_1}{2}), \sin(\frac{\theta_1}{2})\boldsymbol{u_1}]$, 我们希望找出一些中间变换$q_t$, ，让初始变换$q_0$能够平滑地过渡到最终变换$q_1$．𝑡 的取值可以是𝑡 ∈[0,1]

旋转的变化量其实对应的仍是一个旋转。其将由 $q_0$ 变换到 $v_0$ 的向量进一步旋转到 $v_t$ 这个旋转拥有某一个固定的旋转轴 $\bf u_t$，，我 们只需要缩放这个变换所对应的角度𝜙就能够达到插值的目的了。

我们该怎么获得这个旋转的变化量呢?

考虑一下什么变换Δ𝑞能将已经旋转到$v_0$的向量$v$直接变换到$v_1$， 这其实是一个旋转的复合，我们先进行$q_0$变换，再进行Δ𝑞变换，它们复合的结果 需要等于$q_1$变换， 即
$$
\Delta q q_0 = q_1 \\
\Delta q q_0 q_0 ^{-1} = q_1 q_0 ^{-1}
$$

而所有的旋转$q$都是单位四元数，有$q^{-1} = q^*$，上式又可以写作
$$
\Delta q = q_1 q_0^*
$$

Lerp

$$
q_t = Lerp(q_0, q_1, t) = (1-t)q_0 + tq_1
$$

我们是沿着一条直线（也就是圆上的一个弦）进行插值的，这样 插值出来的四元数并不是单位四元数

Nlerp

虽然这样插值出来的 $q_t$ 并不是单位四元数，但只要将$q_t$除以它的模长 $||q_t||$ 就能够将其转化为一个单位四元数了

$$
\boldsymbol{v}_t = Nlerp(\boldsymbol{v}_0, \boldsymbol{v}_1, t) = \frac{(1-t)\boldsymbol{v}_0 + t \boldsymbol{v}_1}{|| (1-t)\boldsymbol{v}_0 + t \boldsymbol{v}_1||} \
\boldsymbol{q}_t = Nlerp(\boldsymbol{q}_0, \boldsymbol{q}_1, t) = \frac{(1-t)\boldsymbol{q}_0 + t \boldsymbol{q}_1}{|| (1-t)\boldsymbol{q}_0 + t \boldsymbol{q}_1||}
$$
Nlerp 插值仍然存在有一定的问题，当需要插值的弧比较大时，$\boldsymbol{v}_t$的角速 度会有显著的变化．我们可以来看一个例子：

这五个𝑡值将整个弧和弦分割成了四个部分．虽然弦上的四段是等长的，但 是四个弧是完全不相等的．𝑡=0到𝑡=0.25之间的弧（红色）明显比𝑡=0.25 到𝑡 =0.50的弧（蓝色）要短了不少

Slerp

为了解决这个问题，我们可以转而对角度进行线性插值．也就是说，如果 $\boldsymbol{v}_1$ 和$\boldsymbol{v}_2$之间的夹角为θ，那么
$$
\theta_t= (1-t) \cdot 0 + t \theta = t \theta
$$

$$
q_t = Slerp(q_0, q_1, t) = \frac{\sin((1-t)\theta)}{\sin(\theta)} q_0 + \frac{\sin(t\theta)}{\sin(\theta)} q_1
$$

其中，
$$
\theta =\cos^{-1}(q_0 \cdot q_1)
$$
注意，这里的 $q_0 \cdot q_1$ 是点积，其结果是一个标量，计算方法为：
$$
q_0 \cdot q_1 = w_0w_1 + x_0x_1 + y_0 y_1 + z_0z_1
$$
而因为任意两个向量（包括四位四元数向量），它们的点积与它们之间的夹角 $\theta$ 以及它们各自的模长（长度）有关：
$$
q_0 \cdot q_1 = ||q_0|| \cdot ||q_1|| \cos(\theta)
$$

如果我们需要对多个四元数进行插值，对每一对四元数使 用Slerp 插值虽然能够保证每两个四元数之间的角速度是固定的，但是角速 度会在切换插值的四元数时出现断点，或者说在切换点不可导。

Squad

$$
Squad(q_0, q_1, q_2, q_3;t) = Slerp(Slerp(q_0, q_3;t),Slerp(q_1, q_2; t); 2t(1-t))
$$

常见 API

1

public static Quaternion LookRotation (Vector3 forward, Vector3 upwards= Vector3.up);

使用指定的 forward 和 upwards 方向创建旋转。 本地的 Z 轴将与给定的，世界中的forward向量对齐，本地的X 轴与 forward 和 upwards 之间的差积对齐，Y 轴与 Z 和 X 之间的差积对齐。

1
2
3
4
5
6
7
8
9
10
11
12
13

public class Test: MonoBehaviour{
    public Transform sphere;

    void Update(){
        Vector3 dir = sphere.position - transform.position;  //正方体指向球体的向量dir = 球体坐标 - 正方体坐标
        Quaternion ang = Quaternion.LookRotation(dir);  //创建一个 使正方体朝向球体的旋转角
        transform.rotation = ang;  //使正方体朝向球体

        Debug.DrawRay(transform.position, transform.forward * 100, Color.blue);  //绘制正方体forward
        Debug.DrawRay(transform.position, dir, Color.green);  //绘制向量dir
        Debug.DrawRay(transform.position, ang.eulerAngles, Color.red);
    }
}

我们需要构建这样一个坐标系，换言之，其被“旋转为”：

• Z轴（前方向，z_axis），也就是输入的forward

• X轴（右方向， x_axis）,此轴追至于刚刚算出来的Z轴，并垂直于upwards， 我们通过叉乘得到

  1	Vector3 x_axis = Vector3.Normalize(Vector3.Cross(upwards, z_axis));

• Y轴（上方向，y_axis），此轴垂直于刚刚运算得到的Z轴与X轴，

  1	y_axis = Vector3.Cross(z_axis, x_axis);

我们期望的旋转矩阵$M$的作用：

我们希望这个矩阵 $M$ 能够将物体的局部坐标系中的向量转换到世界坐标系中。 换句话说，当我们用$M$左乘一个局部坐标向量时，我们应该得到这个向量在世界坐标系中的表示。

也就是说，

• $M \cdot \mathbf{e}{\mathbf{x}{\text{local}}} = M\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$ 此结果为$M$的第一列
• $M \cdot \mathbf{e}{\mathbf{y}{\text{local}}} = M\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}$此结果为$M$的第二列
• $M \cdot \mathbf{e}{\mathbf{z}{\text{local}}} = M\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$此结果为$M$的第三列

一个从A坐标系到B坐标系的变换矩阵，其列向量就是A坐标系的基向量在B坐标系中的表示。即使不存在一组欧拉角能够精确构成这个特定的变换矩阵 $M$

$$ M = \begin{bmatrix} x_{axis}.x & y_{axis}.x & z_{axis}.x \\ x_{axis}.y & y_{axis}.y & z_{axis}.y \\ x_{axis}.z & y_{axis}.z & z_{axis}.z \end{bmatrix} $$

假设A是标准的右手坐标系。考虑一个简单的反射变换 $M = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$ (沿YZ平面反射，即X轴反向)。 A的X轴 $(1,0,0)_A$ 变换后是 $(-1,0,0)_B$ —— 这是 $M$ 的第一列。 A的Y轴 $(0,1,0)_A$ 变换后是 $(0,1,0)_B$ —— 这是 $M$ 的第二列。 A的Z轴 $(0,0,1)_A$ 变换后是 $(0,0,1)_B$ —— 这是 $M$ 的第三列。 由 ${(-1,0,0)_B, (0,1,0)_B, (0,0,1)_B}$ 构成的坐标系B现在是一个左手坐标系。