Complex number & Quaternion

Refer to: quaternion.pdf quaternion by Krasjet

坐标系

本文将使用右手坐标系统， 用右手定则来定义旋转的正方向，即右手拇指指向旋转轴的 $\bf{u}$ 的正方向，这时其它 四个手指弯曲的方向即为旋转的正方向。

基础

• 点乘，标量积

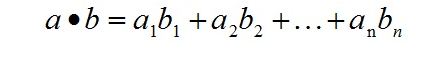
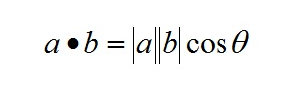
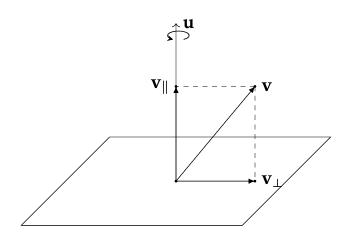
可以看到，$\boldsymbol{v}_{||}$其实就是 $\boldsymbol{v}$ 在 $\boldsymbol{u}$ 上的正交投影(OrthogonalProjection)，根据 正交投影的公式，我们可以得出：

我们需要处理正交于 $\boldsymbol{u}$ 的 $\bf v_{\perp}$

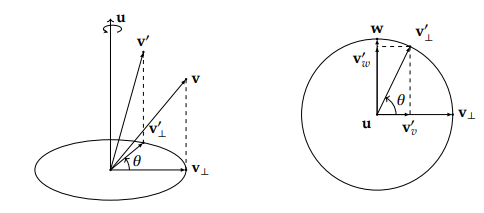
方向永远垂直于矢量ab所在的平面啊。具体方向由右手定则决定。四指跟从向量A和B的旋转方向时，大拇指所朝的方向。

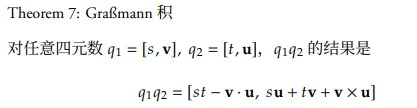
对于四元数 $q = a + bi +cj + dk$， $i^{2} = j^{2} = k^{2} = ijk = -1$

逆和共轭

$q^{-1}$是$q$的逆，规定：
$$
qq^{-1} = q^{-1} q = 1 (q \neq 0)
$$
有
$$
(pq)q^{-1} = p(qq^{-1}) = p \cdot 1 = p \
q^{-1}(qp) = (q^{-1}q)p = 1 \cdot p = p
$$

如果 $|| q || = 1$， 也就是说 $q$ 是一个单位四元数，那么
$$
q^{-1} = \frac{q ^*}{1^{2}} = q^* = [s, \bf{-v}]
$$

旋转

换言之，当我们有 $q= [\cos(\theta), \sin(\theta)\bf{u}]$时，那么$v’ = qvq^*$ 可以将 $\bf{v}$ 沿着 $\bf{u}$ 旋转 2$\theta$ 度。

我们把 $\bf{v}$ 写作一个纯四元数，然后按照四元数乘法进行运算，注意，四元数乘法有结合律，但四元数乘法通常没有交换律。

左乘一个四元数 $q = a + bi +cj + dk$ 等同于左乘下面这个矩阵：
$$
L(q) = \begin{bmatrix}
a & -b & -c & -d \\
b & a & -d & c \\
c & d & a & -b \\
d & -c & b & a
\end{bmatrix}
$$

右乘 $q$ 等同于这个左乘这个矩阵：
$$
R(q) = \begin{bmatrix}
a & -b & -c & -d \\
b & a & d & -c \\
c & -d & a & b \\
d & c & -b & a
\end{bmatrix}
$$

我们有：$qvq^* = L(q)R(q^*)v = R(q^*)L(q)v$, 注意$R(q^*) = R(q)^{T}$

也就是：
$$
qvq^* = \begin{bmatrix}
1 & 0 & 0 & 0 \
0 & 1 - 2c^2 - 2d^2{} & 2bc - 2ad & 2ac + 2bd \
0 & 2bc + 2ad & 1 - 2b^2 - 2d^2 & 2cd - 2ab \
0 & 2bd - 2ac & 2ab + 2cd & 1 - 2b^2 - 2c^2
\end{bmatrix} v
$$

四元数， 轴-角， 旋转矩阵， 欧拉角转换

任意向量 $\bf{v}$ 沿着以单位向量定义的旋转轴 $\bf{u}$ 旋转 $\theta$ 角度之后的 $\bf{v’}$ 可以使用矩阵乘法来获得。

令 $v = [0, \boldsymbol{v} ], q = [\cos(\frac{\theta}{2}), \sin(\frac{\theta}{2})\boldsymbol{u}]$

四元数与3D旋转的关系并不是一对一的，同一个3D旋转可以使用两个不同的四元数来表示。
对于任意的$q = [\cos(\frac{\theta}{2}), \sin(\frac{\theta}{2})\boldsymbol{u}]$，$q$与$-q$ 代表的是同一个旋转。如果𝑞表示的是沿着旋转轴$\bf{u}$旋转θ度，那么−𝑞代表的是沿着相反的旋转轴$- \bf{u}$旋转(2𝜋−θ)度。

对于常见的 ZYX 顺序（Unity Inspector 中使用的顺序，对应先绕Y轴，再绕X轴，再绕Z轴应用旋转，或者说物体先绕自身的Z轴，再绕自身新的X轴，再绕自身新的Y轴）： $q_X=[cos(α/2),sin(α/2)(1,0,0)]$ $q_Y=[cos(β/2),sin(β/2)(0,1,0)]$ $q_Z=[cos(γ/2),sin(γ/2)(0,0,1)]$ 最终的四元数 $q=q_Y⋅q_X⋅q_Z$ (注意乘法顺序，取决于欧拉角的具体定义是内旋还是外旋，以及轴的顺序)。

这个转换是明确的：给定一组特定顺序的欧拉角，总能计算出唯一的一个四元数（不考虑 q 和 −q 的等价性）。

插值

假设有两个旋转变换 $q_0 = [\cos(\frac{\theta_0}{2}), \sin(\frac{\theta_0}{2})\boldsymbol{u_0}]$, $q_1 = [\cos(\frac{\theta_1}{2}), \sin(\frac{\theta_1}{2})\boldsymbol{u_1}]$, 我们希望找出一些中间变换$q_t$, ，让初始变换$q_0$能够平滑地过渡到最终变换$q_1$．𝑡 的取值可以是𝑡 ∈[0,1]

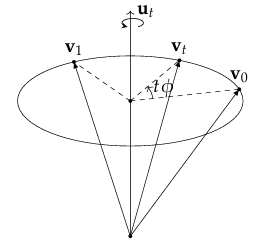
旋转的变化量其实对应的仍是一个旋转。其将由 $q_0$ 变换到 $v_0$ 的向量进一步旋转到 $v_t$ 这个旋转拥有某一个固定的旋转轴 $\bf u_t$，，我 们只需要缩放这个变换所对应的角度𝜙就能够达到插值的目的了。

我们该怎么获得这个旋转的变化量呢?

考虑一下什么变换Δ𝑞能将已经旋转到$v_0$的向量$v$直接变换到$v_1$， 这其实是一个旋转的复合，我们先进行$q_0$变换，再进行Δ𝑞变换，它们复合的结果 需要等于$q_1$变换， 即
$$
\Delta q q_0 = q_1 \\
\Delta q q_0 q_0 ^{-1} = q_1 q_0 ^{-1}
$$

而所有的旋转$q$都是单位四元数，有$q^{-1} = q^*$，上式又可以写作
$$
\Delta q = q_1 q_0^*
$$

Lerp

$$
q_t = Lerp(q_0, q_1, t) = (1-t)q_0 + tq_1
$$

我们是沿着一条直线（也就是圆上的一个弦）进行插值的，这样 插值出来的四元数并不是单位四元数

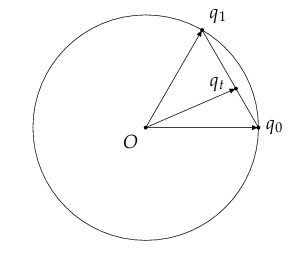
Nlerp

虽然这样插值出来的 $q_t$ 并不是单位四元数，但只要将$q_t$除以它的模长 $||q_t||$ 就能够将其转化为一个单位四元数了

$$
\boldsymbol{v}_t = Nlerp(\boldsymbol{v}_0, \boldsymbol{v}_1, t) = \frac{(1-t)\boldsymbol{v}_0 + t \boldsymbol{v}_1}{|| (1-t)\boldsymbol{v}_0 + t \boldsymbol{v}_1||} \
\boldsymbol{q}_t = Nlerp(\boldsymbol{q}_0, \boldsymbol{q}_1, t) = \frac{(1-t)\boldsymbol{q}_0 + t \boldsymbol{q}_1}{|| (1-t)\boldsymbol{q}_0 + t \boldsymbol{q}_1||}
$$
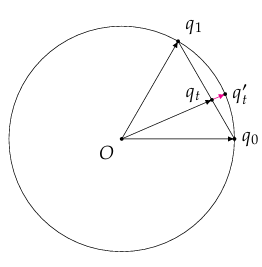
Nlerp 插值仍然存在有一定的问题，当需要插值的弧比较大时，$\boldsymbol{v}_t$的角速 度会有显著的变化．我们可以来看一个例子：

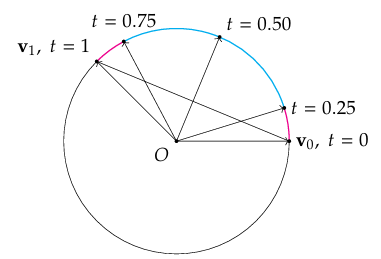
这五个𝑡值将整个弧和弦分割成了四个部分．虽然弦上的四段是等长的，但 是四个弧是完全不相等的．𝑡=0到𝑡=0.25之间的弧（红色）明显比𝑡=0.25 到𝑡 =0.50的弧（蓝色）要短了不少

Slerp

为了解决这个问题，我们可以转而对角度进行线性插值．也就是说，如果 $\boldsymbol{v}_1$ 和$\boldsymbol{v}_2$之间的夹角为θ，那么
$$
\theta_t= (1-t) \cdot 0 + t \theta = t \theta
$$

$$
q_t = Slerp(q_0, q_1, t) = \frac{\sin((1-t)\theta)}{\sin(\theta)} q_0 + \frac{\sin(t\theta)}{\sin(\theta)} q_1
$$

其中，
$$
\theta =\cos^{-1}(q_0 \cdot q_1)
$$
注意，这里的 $q_0 \cdot q_1$ 是点积，其结果是一个标量，计算方法为：
$$
q_0 \cdot q_1 = w_0w_1 + x_0x_1 + y_0 y_1 + z_0z_1
$$
而因为任意两个向量（包括四位四元数向量），它们的点积与它们之间的夹角 $\theta$ 以及它们各自的模长（长度）有关：
$$
q_0 \cdot q_1 = ||q_0|| \cdot ||q_1|| \cos(\theta)
$$

如果我们需要对多个四元数进行插值，对每一对四元数使 用Slerp 插值虽然能够保证每两个四元数之间的角速度是固定的，但是角速 度会在切换插值的四元数时出现断点，或者说在切换点不可导。

Squad

$$
Squad(q_0, q_1, q_2, q_3;t) = Slerp(Slerp(q_0, q_3;t),Slerp(q_1, q_2; t); 2t(1-t))
$$

常见 API

public static Quaternion LookRotation (Vector3 forward, Vector3 upwards= Vector3.up);

使用指定的 forward 和 upwards 方向创建旋转。 本地的 Z 轴将与给定的，世界中的forward向量对齐，本地的X 轴与 forward 和 upwards 之间的差积对齐，Y 轴与 Z 和 X 之间的差积对齐。

public class Test: MonoBehaviour{
    public Transform sphere;

    void Update(){
        Vector3 dir = sphere.position - transform.position;  //正方体指向球体的向量dir = 球体坐标 - 正方体坐标
        Quaternion ang = Quaternion.LookRotation(dir);  //创建一个 使正方体朝向球体的旋转角
        transform.rotation = ang;  //使正方体朝向球体

        Debug.DrawRay(transform.position, transform.forward * 100, Color.blue);  //绘制正方体forward
        Debug.DrawRay(transform.position, dir, Color.green);  //绘制向量dir
        Debug.DrawRay(transform.position, ang.eulerAngles, Color.red);
    }
}

我们需要构建这样一个坐标系，换言之，其被“旋转为”：

• Z轴（前方向，z_axis），也就是输入的forward

• X轴（右方向， x_axis）,此轴追至于刚刚算出来的Z轴，并垂直于upwards， 我们通过叉乘得到

  Vector3 x_axis = Vector3.Normalize(Vector3.Cross(upwards, z_axis));

• Y轴（上方向，y_axis），此轴垂直于刚刚运算得到的Z轴与X轴，

  y_axis = Vector3.Cross(z_axis, x_axis);

我们期望的旋转矩阵$M$的作用：

我们希望这个矩阵 $M$ 能够将物体的局部坐标系中的向量转换到世界坐标系中。 换句话说，当我们用$M$左乘一个局部坐标向量时，我们应该得到这个向量在世界坐标系中的表示。

也就是说，

• $M \cdot \mathbf{e}{\mathbf{x}{\text{local}}} = M\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$ 此结果为$M$的第一列
• $M \cdot \mathbf{e}{\mathbf{y}{\text{local}}} = M\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}$此结果为$M$的第二列
• $M \cdot \mathbf{e}{\mathbf{z}{\text{local}}} = M\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$此结果为$M$的第三列

一个从A坐标系到B坐标系的变换矩阵，其列向量就是A坐标系的基向量在B坐标系中的表示。即使不存在一组欧拉角能够精确构成这个特定的变换矩阵 $M$

$$ M = \begin{bmatrix} x_{axis}.x & y_{axis}.x & z_{axis}.x \\ x_{axis}.y & y_{axis}.y & z_{axis}.y \\ x_{axis}.z & y_{axis}.z & z_{axis}.z \end{bmatrix} $$

假设A是标准的右手坐标系。考虑一个简单的反射变换 $M = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$ (沿YZ平面反射，即X轴反向)。 A的X轴 $(1,0,0)_A$ 变换后是 $(-1,0,0)_B$ —— 这是 $M$ 的第一列。 A的Y轴 $(0,1,0)_A$ 变换后是 $(0,1,0)_B$ —— 这是 $M$ 的第二列。 A的Z轴 $(0,0,1)_A$ 变换后是 $(0,0,1)_B$ —— 这是 $M$ 的第三列。 由 ${(-1,0,0)_B, (0,1,0)_B, (0,0,1)_B}$ 构成的坐标系B现在是一个左手坐标系。