Simulation Basics

Spring - Damper

$$
f = -k_s \boldsymbol{x} - k_d \boldsymbol{v}
$$
where,
$k_s = \text{spring constant}$

$\boldsymbol{x} = \text{distance from rest state}$
$x = \vert \vert \boldsymbol{x}_1 -\boldsymbol{x}_2 \vert \vert - l$
$\hat{\boldsymbol{d}} = \frac{\boldsymbol{x}_1 - \boldsymbol{x}_2}{\vert \vert\boldsymbol{x}_1 - \boldsymbol{x}_2 \vert \vert}$
$\boldsymbol{x} = x\hat{\boldsymbol{d}}$

$k_d = \text{damping factor}$
$\boldsymbol{v} = \text{velocity along spring axis}$

Aerodynamic Forces

$f_{drag} = \frac{1}{2} \rho \vert \vert \boldsymbol{v}\vert \vert ^2 c_d A \hat{\boldsymbol{v}}$

$f_{lift} = \frac{1}{2} \rho \vert \vert \boldsymbol{v}\vert \vert ^2 c_L S(\alpha - \alpha_0)$

Simulation

General Steps

1. Compute all forces acting on each particle in the
   system in the current configuration

2. Compute the resulting acceleration for each particle
   (a=f/m)

3. Integrate over some small time step Dt to get new
   positions and velocities at next time step

4. Repeat

一般的，我们有这样的关系：
$\ddot{\boldsymbol{x}} = \frac{1}{m} \boldsymbol{f(x, \dot{x})}$ 或是，$\dot{\boldsymbol{v}} = \frac{1}{m} \boldsymbol{f(x, v)}$

可以理解为，当前的加速度由当前的位移与速度决定。例如，在一个弹簧阻尼系统中，当前受到的力是位移和速度共同决定的。

我们往往想要求一阶的表示方式$\boldsymbol{x}(t)$

Phase Space

State Position (6 x 1)
$s = \left[\begin{matrix}
\boldsymbol{x} \ \boldsymbol{v}
\end{matrix}\right]$

State Velocity (6 x 1)
$s = \left[\begin{matrix}
\dot{\boldsymbol{x}} \ \dot{\boldsymbol{v}}
\end{matrix}\right]$

Particle System Dynamics (6 x 1)

$s = \left[\begin{matrix}
\boldsymbol{v} \ \frac{\boldsymbol{f}}{m}
\end{matrix}\right]$

清空旧力 → 计算新力 → 准备数据给求解器 → 用求解器更新粒子状态

Angular Momentum: $\boldsymbol{L} = \boldsymbol{r} \times \boldsymbol{p} = \boldsymbol{r} \times m \boldsymbol{v}$

角动量可以理解为物体旋转的某种“惯性”，它是一种矢量物理量，具有大小和方向

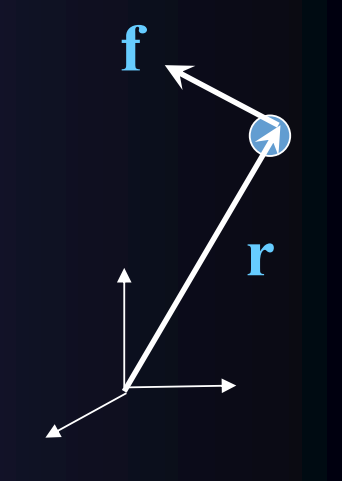
Rate of change of Angular Momentum (力矩/扭矩)

$\boldsymbol{\tau} = \frac{d\boldsymbol{L}}{dt} = \frac{d\boldsymbol{r}}{dt} \times m\boldsymbol{v} + \boldsymbol{r} \times m \frac{d\boldsymbol{v}}{dt}$

$\boldsymbol{\tau} = \boldsymbol{r} \times \boldsymbol{f}
$
力与力臂的乘积

velocity of the particle:
$\boldsymbol{v} = \frac{d\boldsymbol{r}}{dt} = \omega \times r$

当一个刚体绕固定轴旋转时，其上的点做的是圆周运动。圆周运动的速度方向是切线方向，可以通过角速度的叉乘表达出来。

$$
\mathbf{v} = \frac{d\mathbf{r}}{dt} = \dot{\mathbf{r}} = \boldsymbol{\omega} \times \mathbf{r}
$$

Acceleration:

$$
\mathbf{a} = \frac{d\mathbf{v}}{dt} = \frac{d\boldsymbol{\omega}}{dt} \times \mathbf{r} + \boldsymbol{\omega} \times \frac{d\mathbf{r}}{dt}
$$

$$
\quad = \dot{\boldsymbol{\omega}} \times \mathbf{r} + \boldsymbol{\omega} \times (\boldsymbol{\omega} \times \mathbf{r})
$$

当角加速度为零时：
$$\dot{\boldsymbol{\omega}} = 0 $$

• Centripetal acceleration
  $$
  \mathbf{a} = \boldsymbol{\omega} \times (\boldsymbol{\omega} \times \mathbf{r})
  $$

• Centrifugal force
  $$
  \mathbf{f}_{\text{centrifugal}} = -m \boldsymbol{\omega} \times (\boldsymbol{\omega} \times \mathbf{r})
  $$

If the length of $\mathbf{r}$ is changing as a function of time then,
Velocity:

$$
\mathbf{v} = \frac{d\mathbf{r}}{dt} = \boldsymbol{\omega} \times \mathbf{r} + \mathbf{v}_r
$$

Acceleration:

$$
\frac{d\mathbf{v}}{dt} = \frac{d\boldsymbol{\omega}}{dt} \times \mathbf{r}

• \boldsymbol{\omega} \times \frac{d\mathbf{r}}{dt}
• \frac{d\mathbf{v}_r}{dt}
  $$

$$
= \dot{\boldsymbol{\omega}} \times \mathbf{r}

• \boldsymbol{\omega} \times \dot{\mathbf{r}}
• \dot{\mathbf{v}}_r
  $$

因为：

$$
\dot{\mathbf{r}} = \boldsymbol{\omega} \times \mathbf{r} + \mathbf{v}_r
$$

所以：

$$
\mathbf{a} = \dot{\boldsymbol{\omega}} \times \mathbf{r}

• \boldsymbol{\omega} \times (\boldsymbol{\omega} \times \mathbf{r})
• \dot{\mathbf{v}}_r
  $$

Rewriting Angular Momentum
$$
\mathbf{L} = \mathbf{r} \times \mathbf{p} = \mathbf{r} \times (m\mathbf{v}) = m\mathbf{r} \times \mathbf{v}
= m\mathbf{r} \times (\boldsymbol{\omega} \times \mathbf{r}) = -m \mathbf{r} \times \mathbf{r} \times \boldsymbol{\omega}
$$

这里的 𝑟 表示的是：

质点（或物体上某一点）相对于旋转轴/参考点的位置向量。

🔹 Replace $\mathbf{r} \times$ with a cross product equivalent matrix $\boldsymbol{\Gamma}$ , where:
$$
\boldsymbol{\Gamma} =
\begin{bmatrix}
0 & -r_z & r_y \
r_z & 0 & -r_x \
-r_y & r_x & 0
\end{bmatrix}
$$

🔹 This allows:
$$
\mathbf{L} = -m \mathbf{r} \times (\mathbf{r} \times \boldsymbol{\omega}) = -m \boldsymbol{\Gamma} \cdot \boldsymbol{\Gamma} \cdot \boldsymbol{\omega}
$$

🔹 Define Moment of Inertia Matrix:
$$
\mathbf{I} = -m \boldsymbol{\Gamma} \cdot \boldsymbol{\Gamma}
$$

🔹 Results in the Angular Momentum equation:
$$
\mathbf{L} = \mathbf{I} \cdot \boldsymbol{\omega}
$$

Integration

当我们知道一个关系后，例如first-order ODE form：

$\dot{\boldsymbol{x}} = \boldsymbol{f(x,u)}$ ，我们想知道 $\boldsymbol{x}(t)$

根据泰勒展开公式，有
$$\mathbf{x}(t_0 + \Delta t) =
\mathbf{x}(t_0) +
\frac{d\mathbf{x}}{dt}(t_0) \Delta t +
\frac{1}{2!} \frac{d^2 \mathbf{x}}{dt^2}(t_0) \Delta t^2 +
\frac{1}{3!} \frac{d^3 \mathbf{x}}{dt^3}(t_0) \Delta t^3 + \cdots$$

换一种写法：用离散帧时间 $t_k$

可以把时间离散成一帧一帧（每一帧时长为 $\Delta t$）：

$$\mathbf{x}(t_{k+1}) \approx \mathbf{x}(t_k) +
\dot{\mathbf{x}}(t_k)\Delta t +
\frac{1}{2!} \ddot{\mathbf{x}}(t_k)\Delta t^2 +
\frac{1}{3!} \dot{\ddot{\mathbf{x}}}(t_k)\Delta t^3 + \cdots$$

高次的项可以由链式法则求得

仅保留一阶的项时，有
$$\mathbf{x}(t_{k+1}) \approx \mathbf{x}(t_k) +
\dot{\mathbf{x}}(t_k)\Delta t $$
此处，
$$
\dot{\mathbf{x}}(t_k) = \mathbf{f(x(t_k), u(t_k) )}
$$

这样做的话如果时间间隔过长，会很不稳定。

我们考虑使用 $2^{nd} \text{Order Runge Kutta}$
Step 1.
使用欧拉方法计算 预测值
$
\mathbf{x}^p(t_{k+1}) = \mathbf{x}(t_k) + \dot{\mathbf{x}}(t_k)\Delta t
$
而后，讲此预测值带入到关系中，有

$
\dot{\mathbf{x}}^p(t_{k+1}) = f(\mathbf{x}^p(t_{k+1}), \mathbf{u}(t_k))
$

最后求取一个平均值
$
\mathbf{x}(t_{k+1}) = \mathbf{x}(t_k) + \frac{\Delta t}{2} \left[
\dot{\mathbf{x}}(t_k) + \dot{\mathbf{x}}^p(t_{k+1})
\right]
$

4ᵗʰ Order Runge Kutta

$
\mathbf{x}(t_{k+1}) = \mathbf{x}(t_k) + \frac{1}{6} \left[ \mathbf{d}_1 + 2\mathbf{d}_2 + 2\mathbf{d}_3 + \mathbf{d}_4 \right]
$

---

🔹 Where:

$
\mathbf{d}_1 = \Delta t \cdot \dot{\mathbf{x}}(t_k) = \Delta t \cdot \mathbf{f}(\mathbf{x}(t_k), \mathbf{u}(t_k))
$

$
\mathbf{d}_2 = \Delta t \cdot \mathbf{f} \left(t_k + \frac{\Delta t}{2}, \mathbf{x}(t_k) + \frac{1}{2}\mathbf{d}_1 \right)
$

$
\mathbf{d}_3 = \Delta t \cdot \mathbf{f} \left(t_k + \frac{\Delta t}{2}, \mathbf{x}(t_k) + \frac{1}{2}\mathbf{d}_2 \right)
$

$
\mathbf{d}_4 = \Delta t \cdot \mathbf{f} \left(t_k + \Delta t, \mathbf{x}(t_k) + \mathbf{d}_3 \right)
$

🔁 Backwards Euler:

$
\mathbf{x}(t_k) = \mathbf{x}(t_{k+1}) - \dot{\mathbf{x}}(t_{k+1}) \Delta t
$

or equivalently:

$
\mathbf{x}(t_{k+1}) = \mathbf{x}(t_k) + \dot{\mathbf{x}}(t_{k+1}) \Delta t
$

问题是，我们怎么算 $\dot{\mathbf{x}}(t_{k+1})$

①根据我们已知的关系，
我们${\boldsymbol{\dot {x}}(t_{k+1})} = \boldsymbol{f}(\boldsymbol{x}(t_{k+1}))$
但是我们不知道$\boldsymbol{x}(t_{k+1})$， 我们使用RK2来估算这个值

②一般的，我们使用泰勒展开
$$
\boldsymbol{x}(t_{k+1}) = \boldsymbol x(t_k) + \Delta t \cdot \dot{ \boldsymbol{x}}(t_{k+1}) \ = \boldsymbol{x}(t_{k}) + \Delta \boldsymbol{x}(t_k)
$$
$\dot{\mathbf{x}}(t_{k+1}) = \boldsymbol{f}(\boldsymbol{x}(t_{k+1})) = \boldsymbol{f}(\boldsymbol{x}(t_{k}) + \Delta \boldsymbol{x}(t_k))$

$\boldsymbol{x}(t_{k}) + \Delta \boldsymbol{x}(t_k) = \boldsymbol{x}(t_k) + \Delta t \cdot \boldsymbol{f}(\boldsymbol{x}(t_{k}) + \Delta \boldsymbol{x}(t_k))$

$
\mathbf{x}(t_{k+1}) = \mathbf{x}(t_k) + \Delta \mathbf{x}(t_k)
$

$
\mathbf{x}(t_{k+1}) = \mathbf{x}(t_k) +
\left( \frac{1}{\Delta t} \mathbf{I} - \frac{\partial \mathbf{f}}{\partial \mathbf{x}} (t_k) \right)^{-1}
\mathbf{f}(\mathbf{x}(t_k))
$

设：

$$\mathbf{f}(x, y) =
\begin{bmatrix}
f_1(x, y) = x^2 + y \
f_2(x, y) = \sin(xy)
\end{bmatrix}$$

则 Jacobian 是：

$$\frac{\partial \mathbf{f}}{\partial \mathbf{x}} =
\begin{bmatrix}
\frac{\partial f_1}{\partial x} & \frac{\partial f_1}{\partial y} \
\frac{\partial f_2}{\partial x} & \frac{\partial f_2}{\partial y}
\end{bmatrix}

\begin{bmatrix}
2x & 1 \
y\cos(xy) & x\cos(xy)
\end{bmatrix}$$

Adams Bashforth

🔹 Keep terms up to 2ⁿᵈ order in Taylor series approx

$$
\mathbf{x}(t_{k+1}) = \mathbf{x}(t_k) + \dot{\mathbf{x}}(t_k),\Delta t

• \frac{1}{2!},\ddot{\mathbf{x}}(t_k),\Delta t^2
  $$

---

🔹 Approximate the second derivative as

$$
\ddot{\mathbf{x}}(t_k)
\approx
\frac{\dot{\mathbf{x}}(t_k) - \dot{\mathbf{x}}(t_{k-1})}{\Delta t}
$$

---

🔹 Which yields

$$
\mathbf{x}(t_{k+1})
= \mathbf{x}(t_k)

• \frac{\Delta t}{2},\bigl[3,\dot{\mathbf{x}}(t_k) - \dot{\mathbf{x}}(t_{k-1})\bigr]
  $$

Verlet Integration

🔹 Does not require velocity to be explicitly computed

---

🔹 Given the current value of $\mathbf{x}(t_k)$, compute $\mathbf{x}$ at the next time step $t_{k+1}$ and previous time step $t_{k-1}$using a 2ⁿᵈ order approximation:

$$
\mathbf{x}(t_{k+1}) = \mathbf{x}(t_k) + \dot{\mathbf{x}}(t_k) \Delta t + \frac{1}{2} \ddot{\mathbf{x}}(t_k) \Delta t^2
$$

$$
\mathbf{x}(t_{k-1}) = \mathbf{x}(t_k) - \dot{\mathbf{x}}(t_k) \Delta t + \frac{1}{2} \ddot{\mathbf{x}}(t_k) \Delta t^2
$$

---

🔹 Adding the two together and rearranging yields:

$$
\mathbf{x}(t_{k+1}) = 2\mathbf{x}(t_k) - \mathbf{x}(t_{k-1}) + \ddot{\mathbf{x}}(t_k) \Delta t^2
$$