Curves & Spline
Refer to: The Continuity of Splines by Freya Holmér
- Bernstein
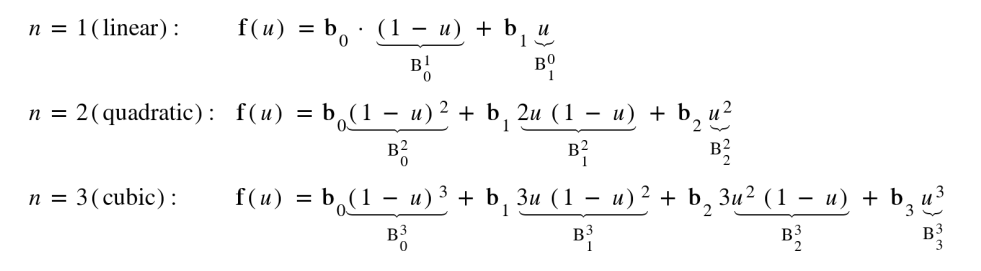
此处,$B_0^{3}$ 等亦可写作 $B_{0,3}(u) = C(3,0) \cdot u ^{0} \cdot (1-u)^{3}$
- DeCasteljau
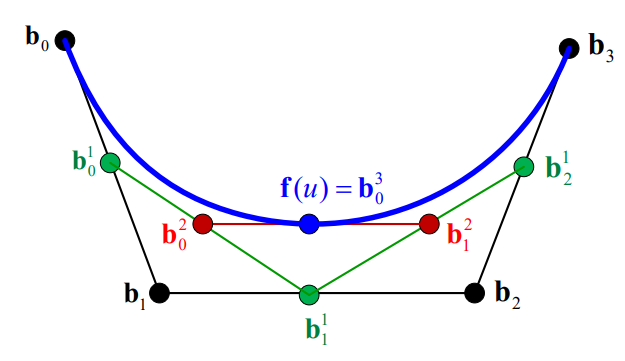
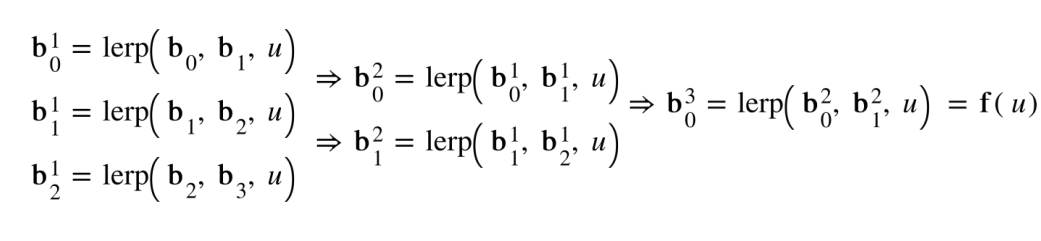
- Polynomial Coefficients
$$
f(u) = b_0 + u(-3b_0 + 3b_1) + u^{2}(3b_0 -6b_1 + 3b_2) + u^{3}(-b_0 + 3b_1 -3b_2 + b_3)
$$
Efficient Evaluation using Horner’s Method:
$$
f(u) = C_0 + u(C_1 + u(C_2 + uC_3))
$$
Subdivision of Bezier Curve

Derivatives of Bezier Curves
For the case where u = 0
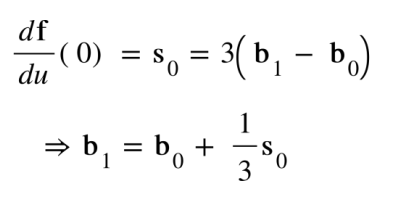
when u = 1
Why Spline?
如果需要我们对一条曲线有更多的控制能力,我们可以考虑提高贝塞尔曲线的次数,例如,一个6次贝塞尔曲线会有7个控制点,其形如:
$$
X(s) = (1-s)^6 P_0 + 6s(1-s)^5 P_1 + 15s^2(1-s)^4 P_2 + 20s^3(1-s)^3 P_3 + 15s^4(1-s)^2 P_4 + 6s^5(1-s) P_5 + s^6 P_6
$$
但是,移动每个控制点的时候,整个曲线都会受到影响,计算也会变得更加复杂。
为了更稳定地计算并获得更好地局部控制线和直观性,我们会将多段较低阶地贝塞尔曲线连接起来。
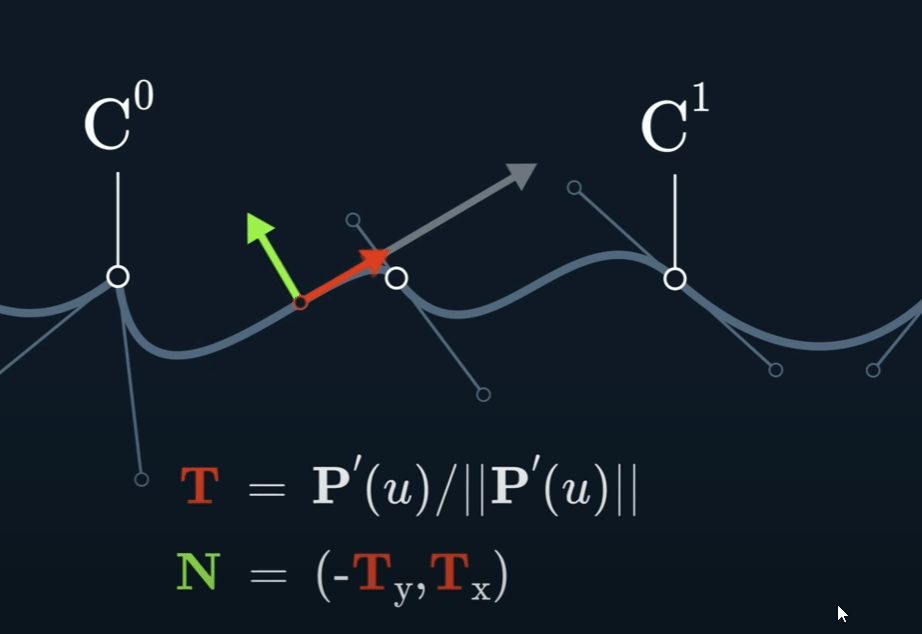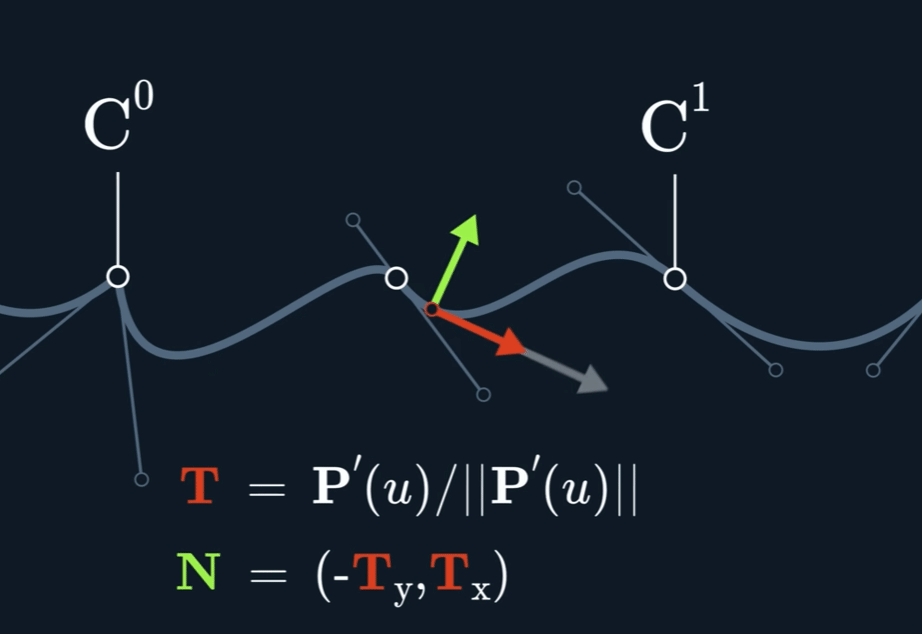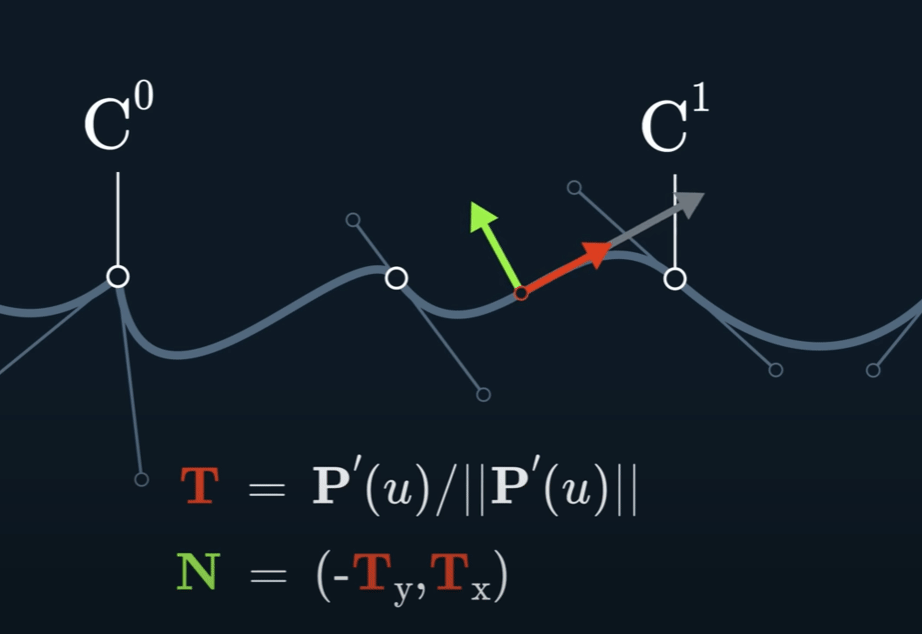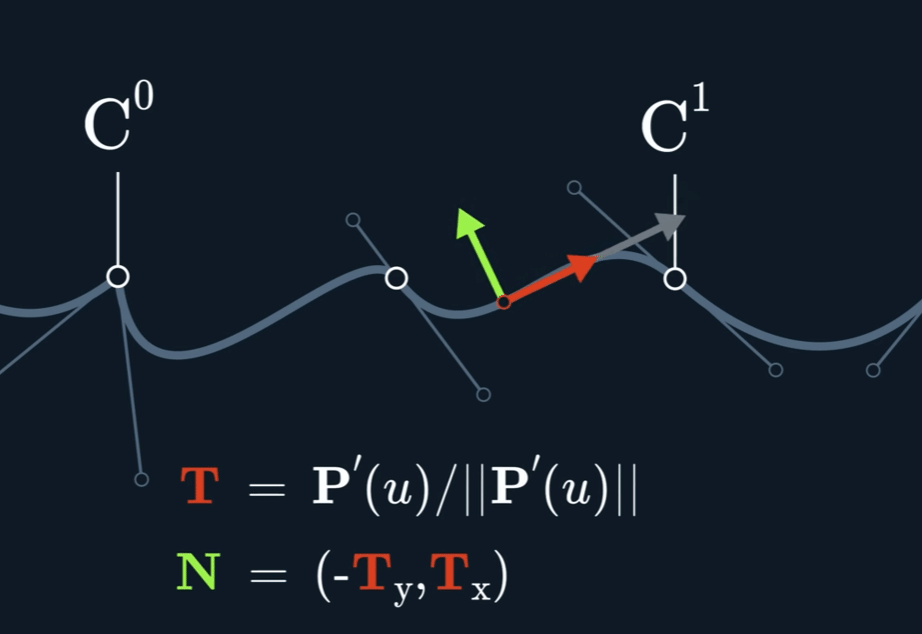
三种切线

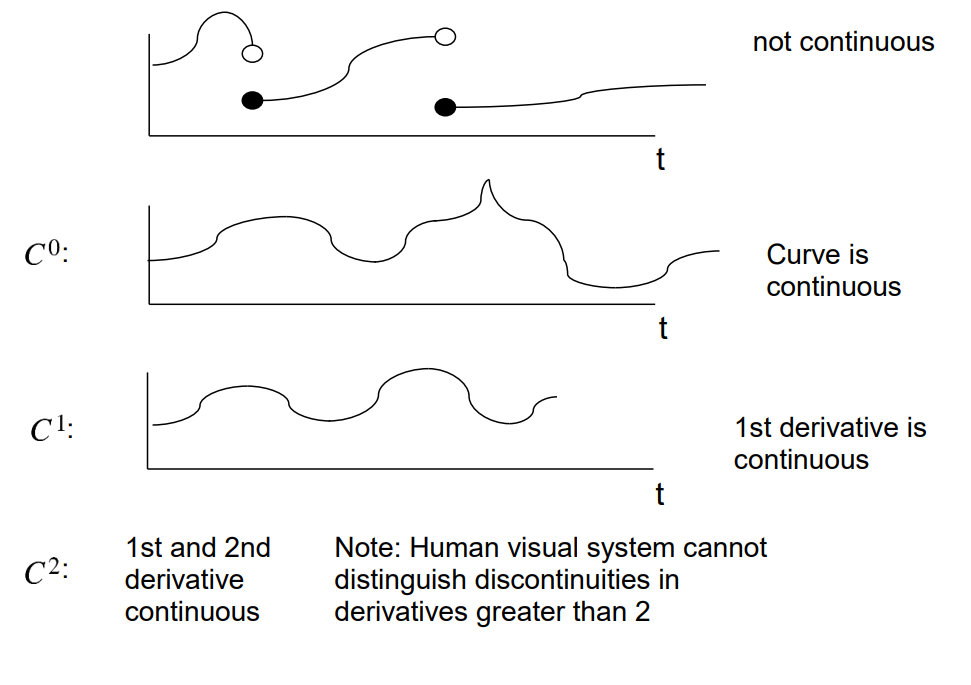
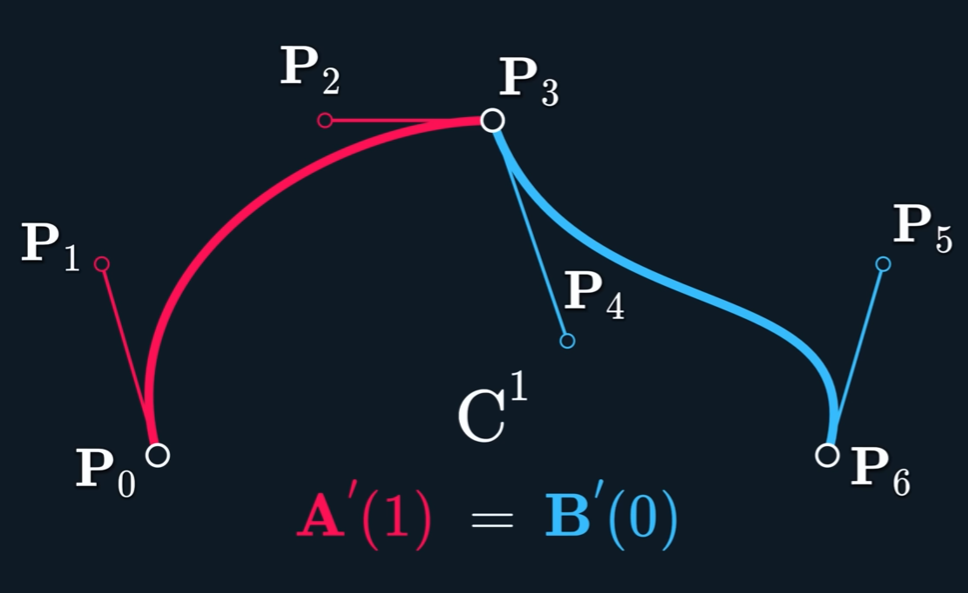
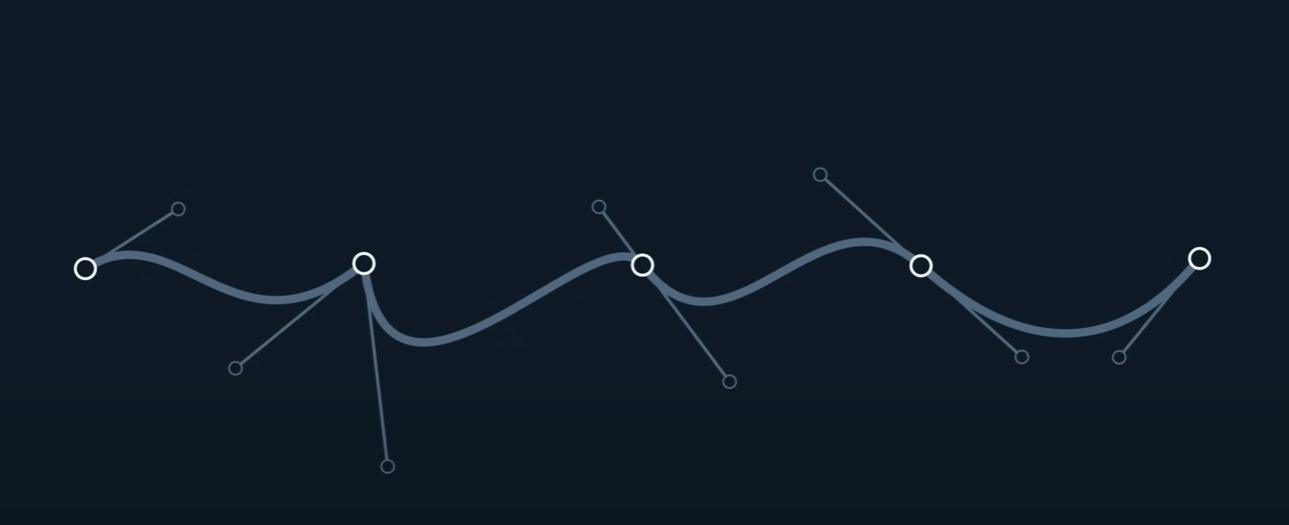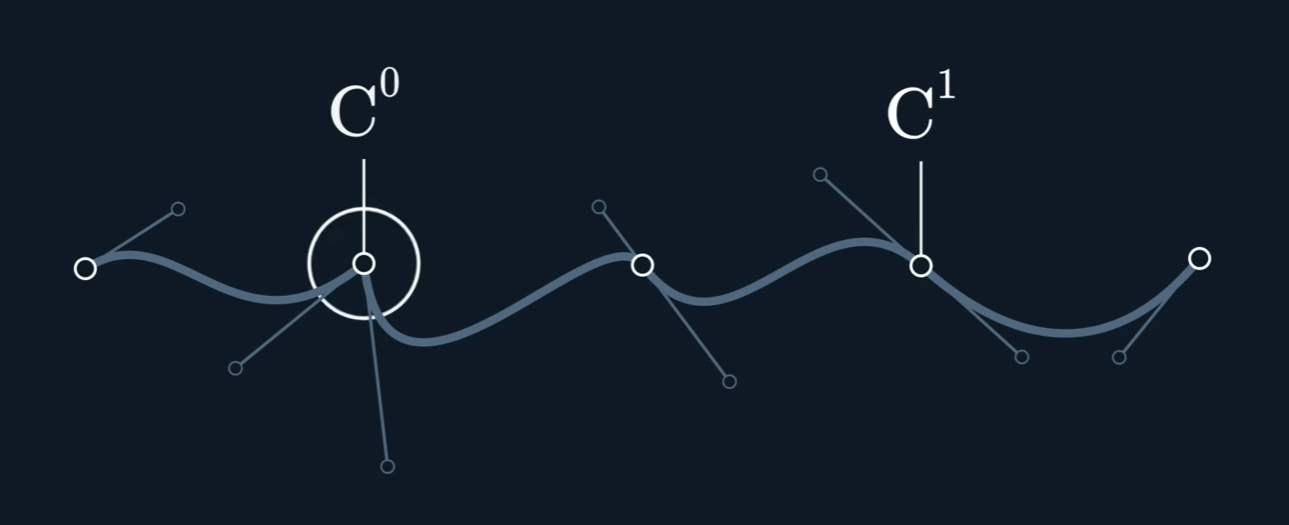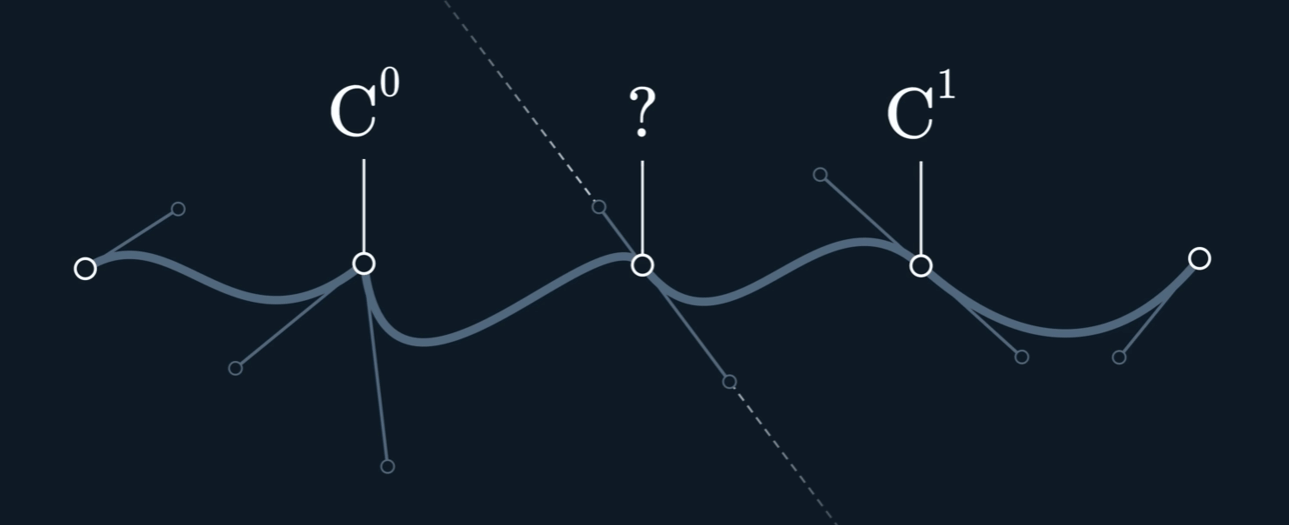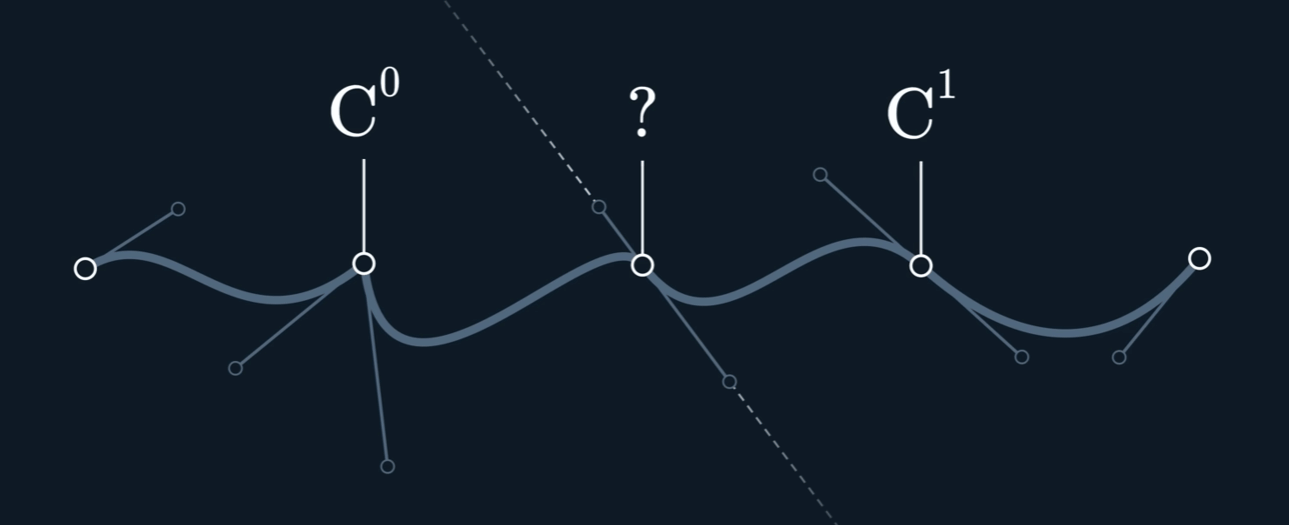
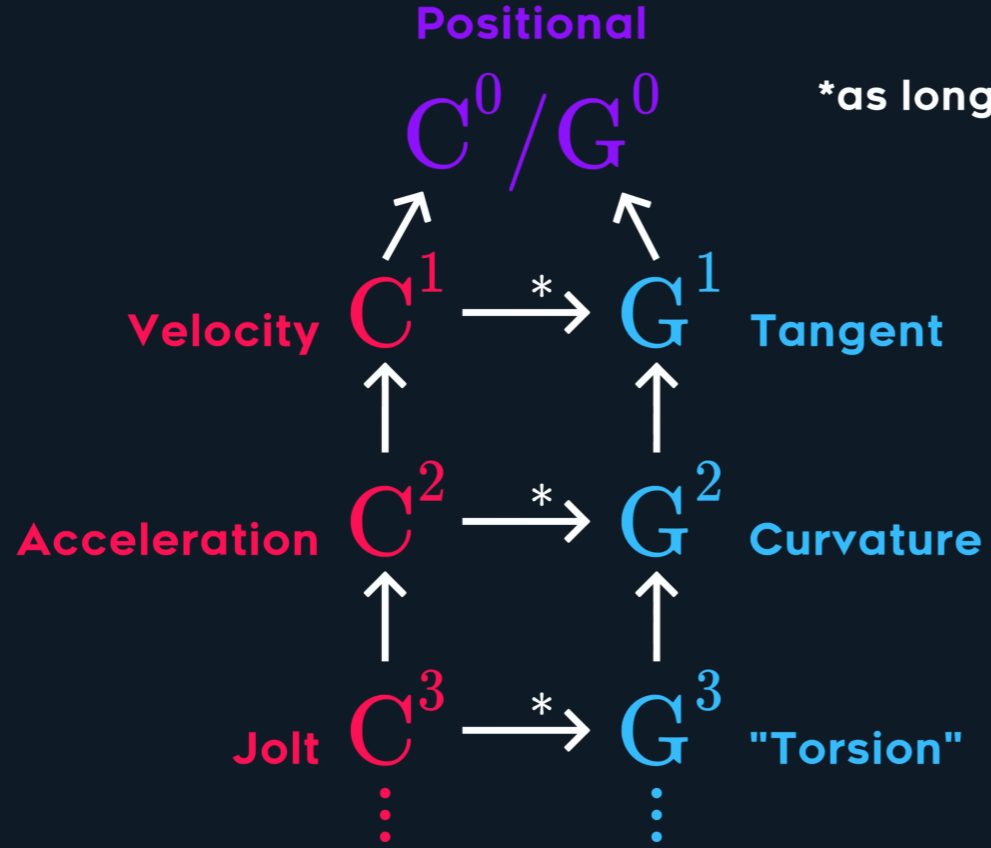
Continuity
$C^{n}$ continuous if $A^{(i)}(t_{end}) = B^{(i)}(t_{start})$ for $i$ in $ {0,…,n}$
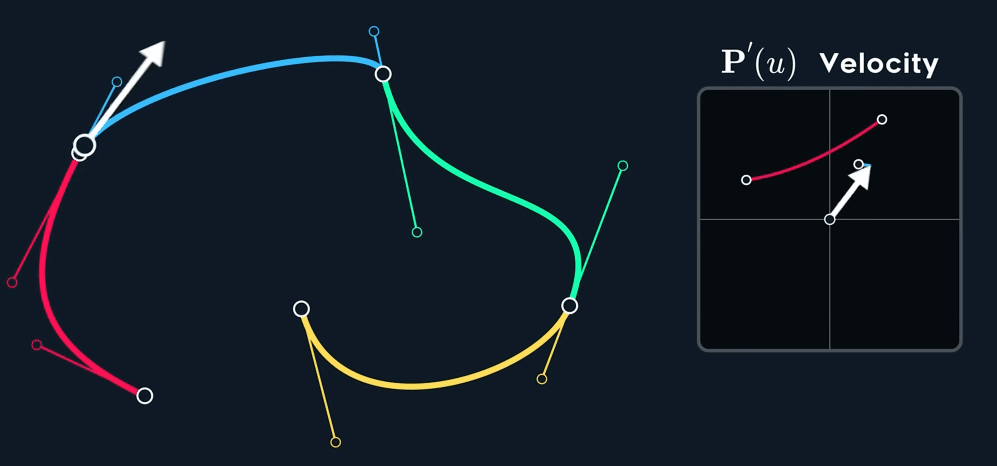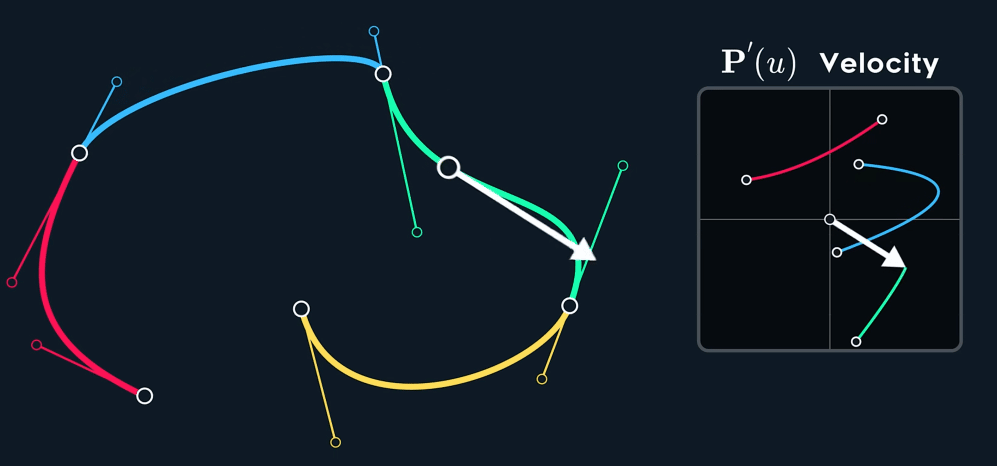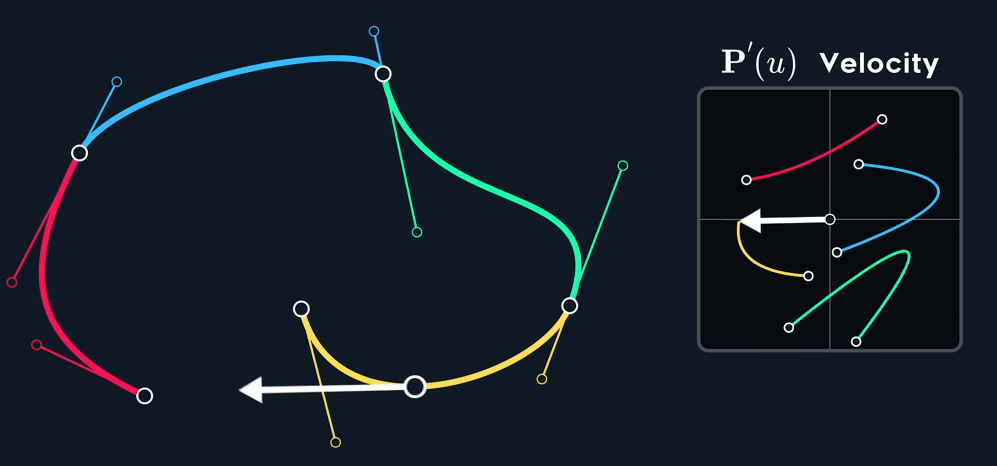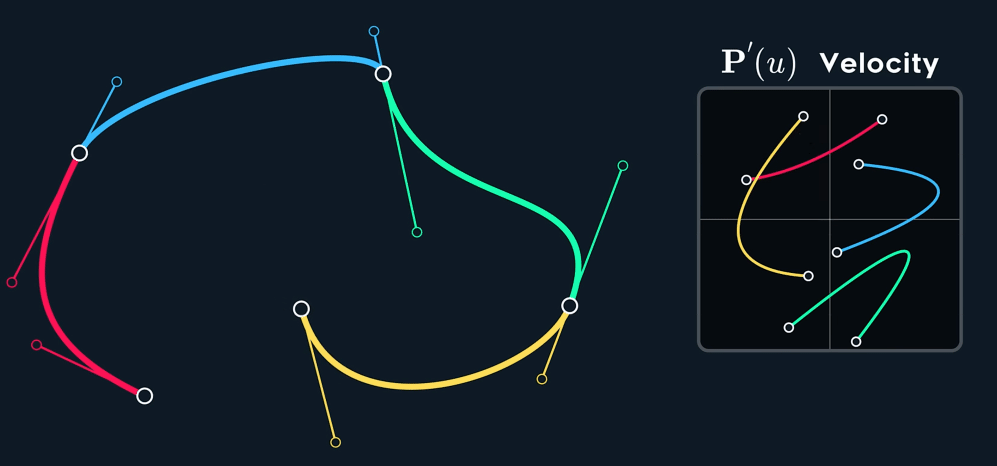
观察下图,可以看到速度并不是连续的,也就是不满足 $C^1$ 连续性。即使原 spline 在 joint 处的两个控制点形成的两个切线已经 aligned (方向相同,但是大小不同)。
当控制点关于 joint 点 mirror 时, $C^1$连续。
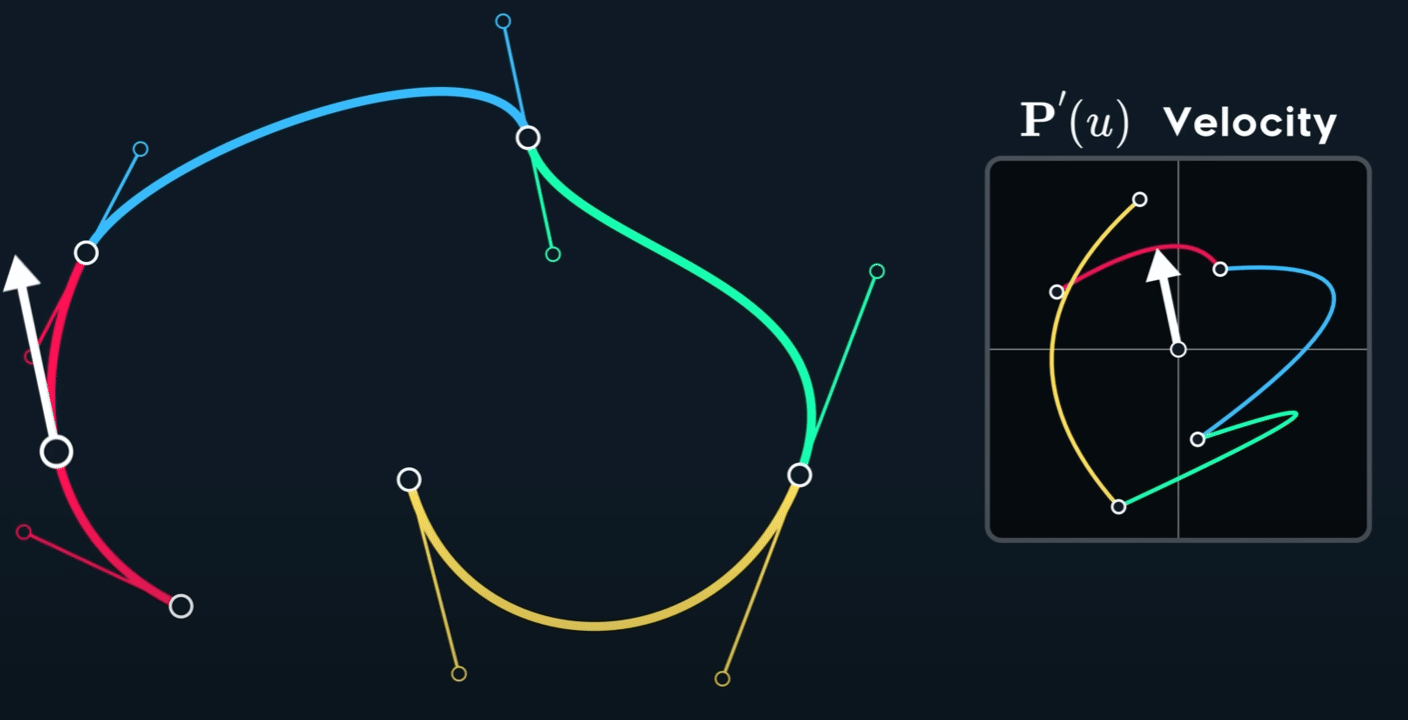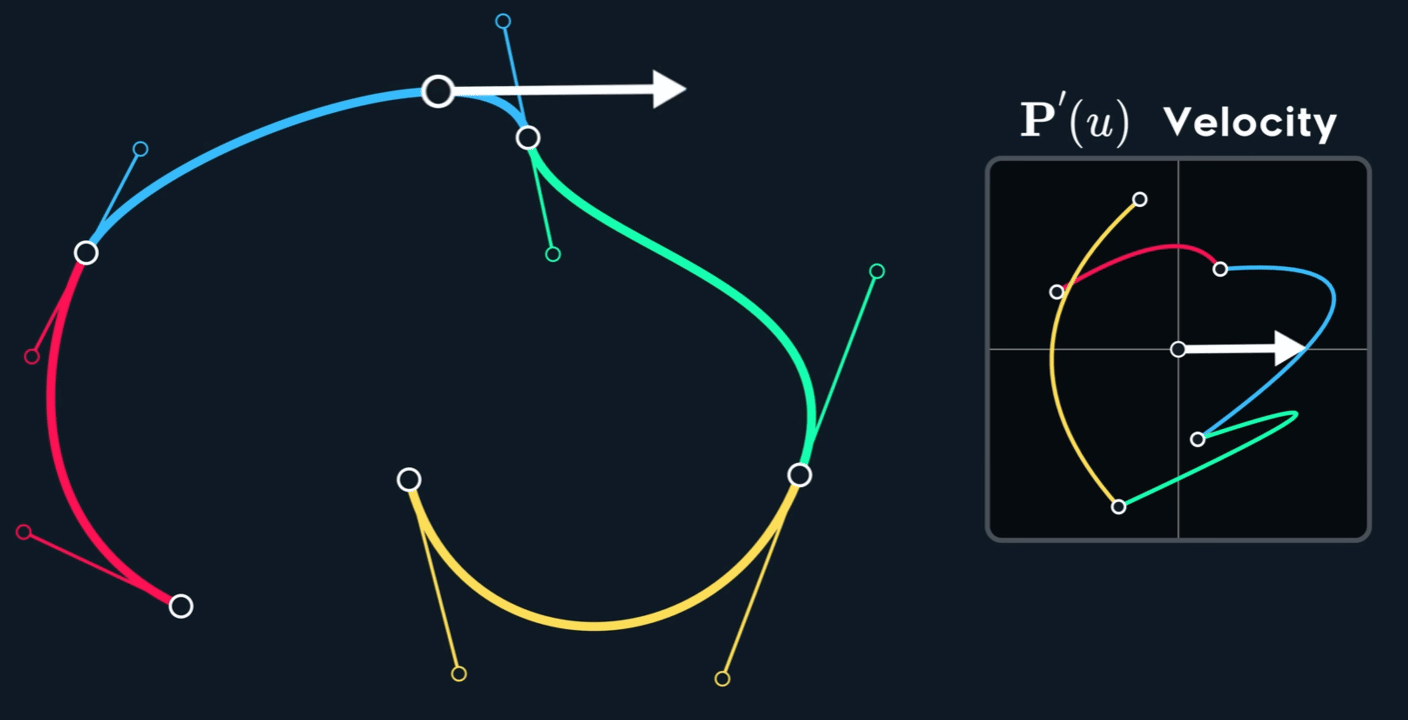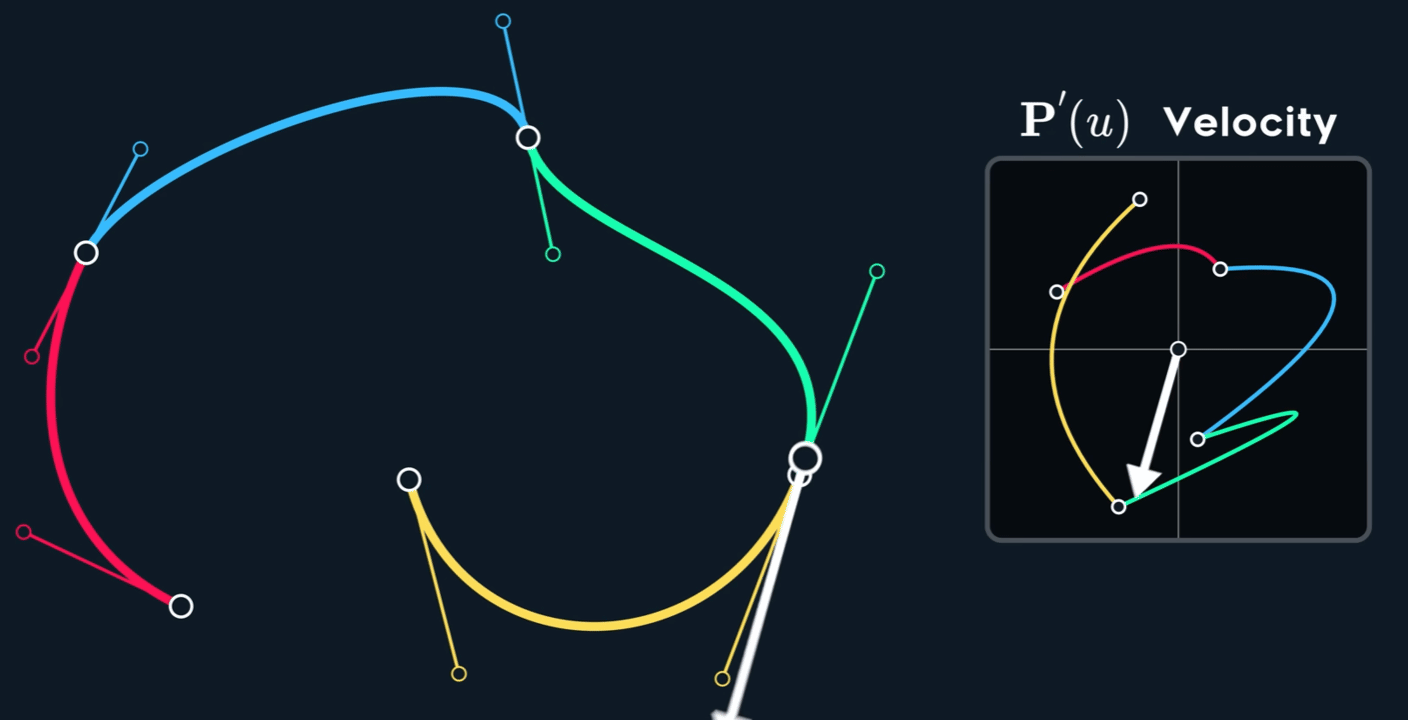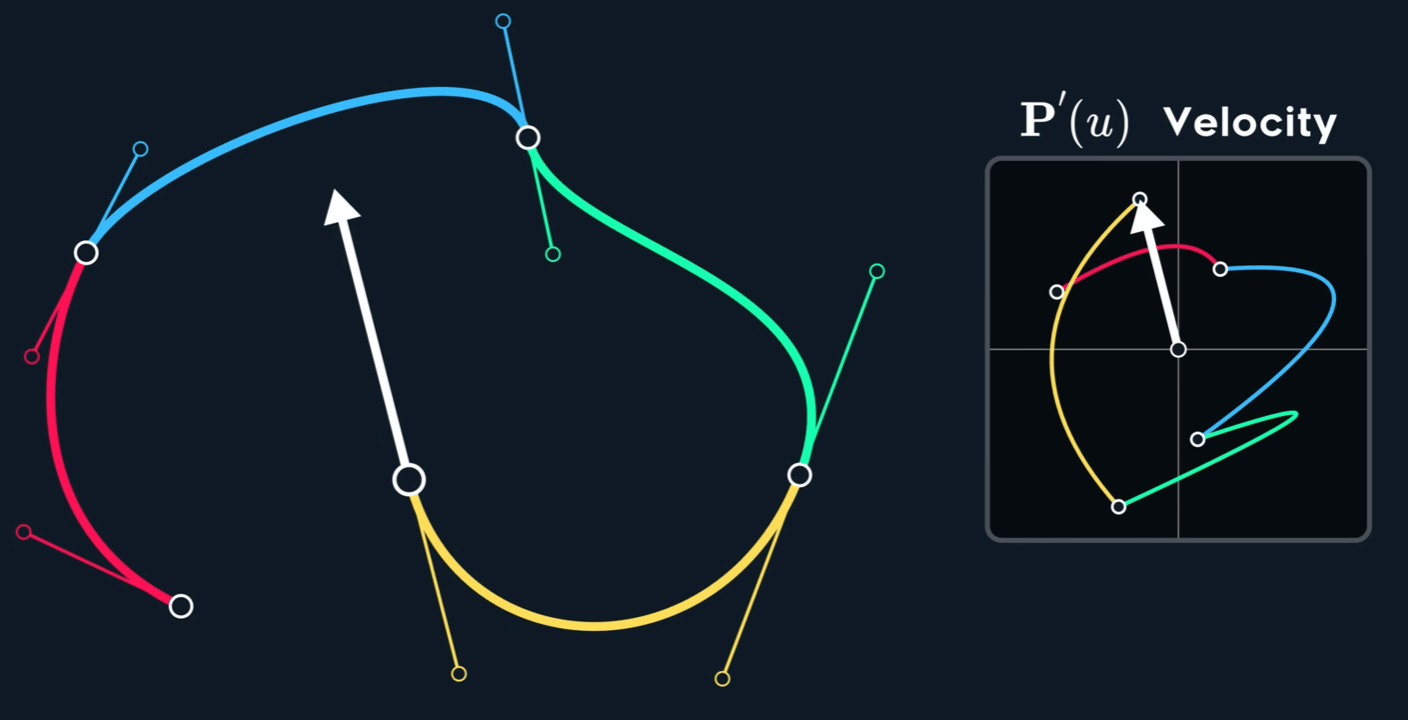
如何构造出 $C^1$ 呢?Mirror 意味着怎么样的关系呢?
我们对一段贝塞尔曲线求导,有
$$
f’(u) = -3b_0 + 3b_1 + 2u(3b_0 -6b_1 + 3b_2) + 3u^2(-b_0 + 3b_1 -3b_2 + b_3)
$$
那么,当$u_0 = 1$时(第一段曲线的右端点)
$$
f’(1) = -3b_2 + 3b_3
$$
当$u_1 = 0$ (第二段曲线的左端点)
$$
f’(0) = -3b_3 + 3b_4
$$
当$f’(1) =f’(0)$时,有
$$
b_4 = 2b_3 - b_2
$$
也就是说,当 Mirror 时,$b_4$ 的位置已经被 $b_2$ 与 $b_3$ 完全决定,不再能被用户自由控制。
$C^2$ 连续性?
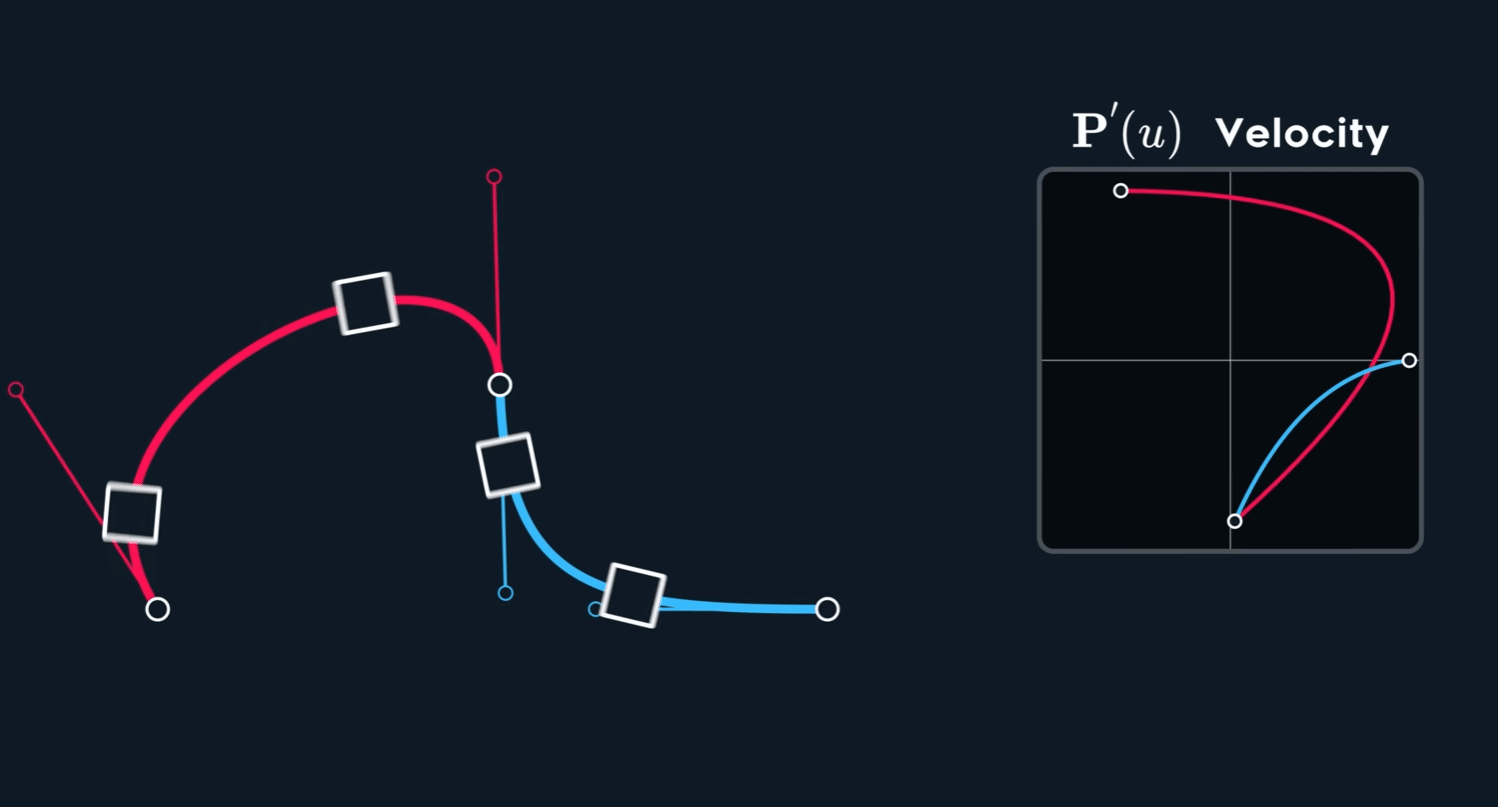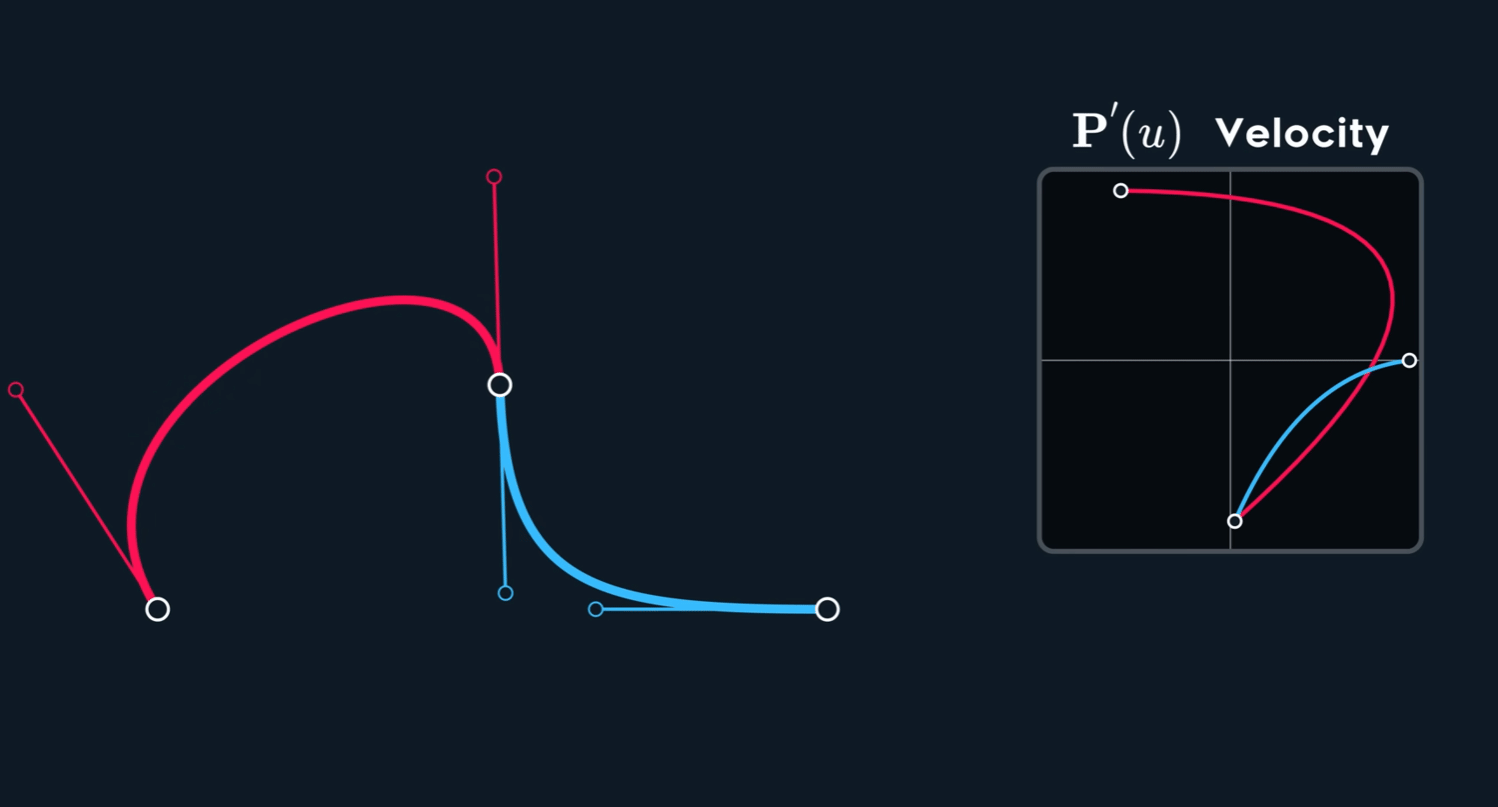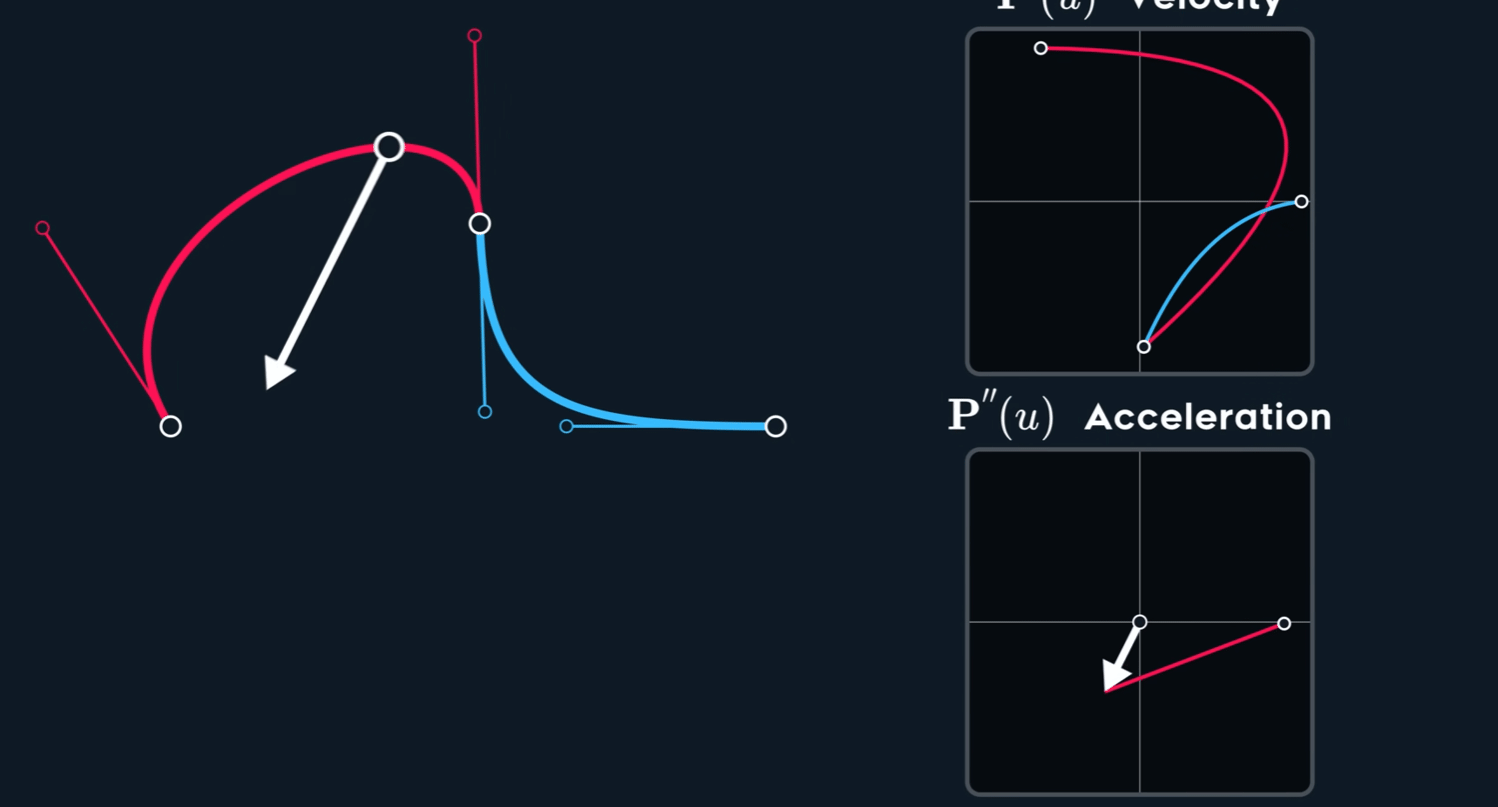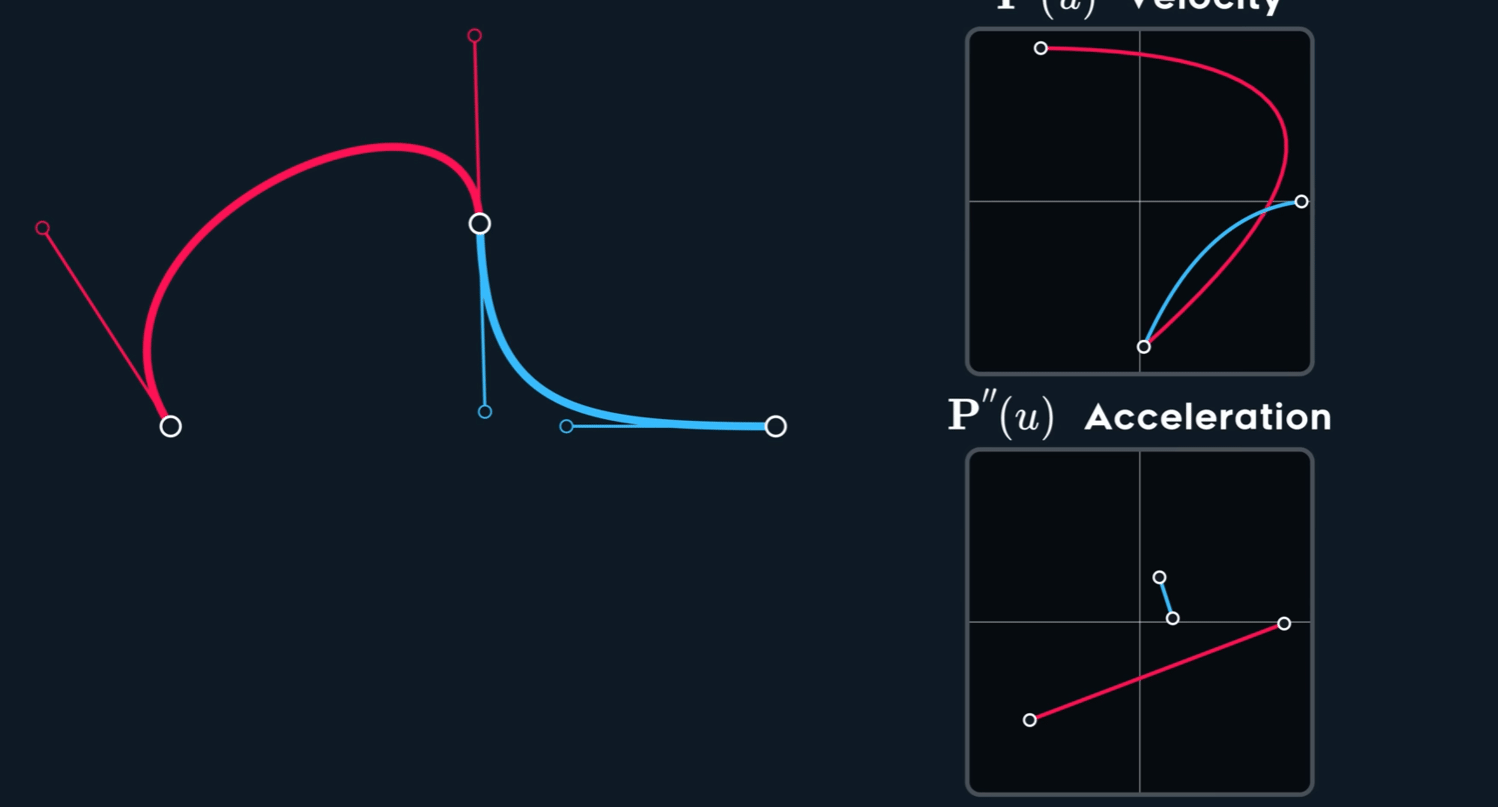
加速度改变速度。
我们对上面提到的速度再求一次导,有
$$
f’’(u) = 6b_0 -12b_1 + 6b_2 + 6u(-b_0 + 3b_1 -3b_2 + b_3)
$$
那么,当$u_0 = 1$时(第一段曲线的右端点)
$$
f’’(1) = 6b_1 - 12b_2 +6 b_3
$$
当$u_1 = 0$ (第二段曲线的左端点)
$$
f’’(0) = 6b_3 -12b_4 + 6b_5
$$
当$f’’(1) =f’(0)$时,有
$$
b_5 = b_1 - 2 b_2 + 2b_4
$$
而$C^{1}$ =又保证了,$b_4$ 已经完全被$b_3$ 与$b_2$ 控制
$$
b_4 = 2b_3 - b_2
$$
所以在$C^{2}$下有
$$
b_5 = b_1 + 4(b_3 - b_2)
$$
也就是说,当 $C^{2}$ 时,$b_5$ 的位置已经被 $b_1$ $b_2$ 与 $b_3$ 完全决定,不再能被用户自由控制。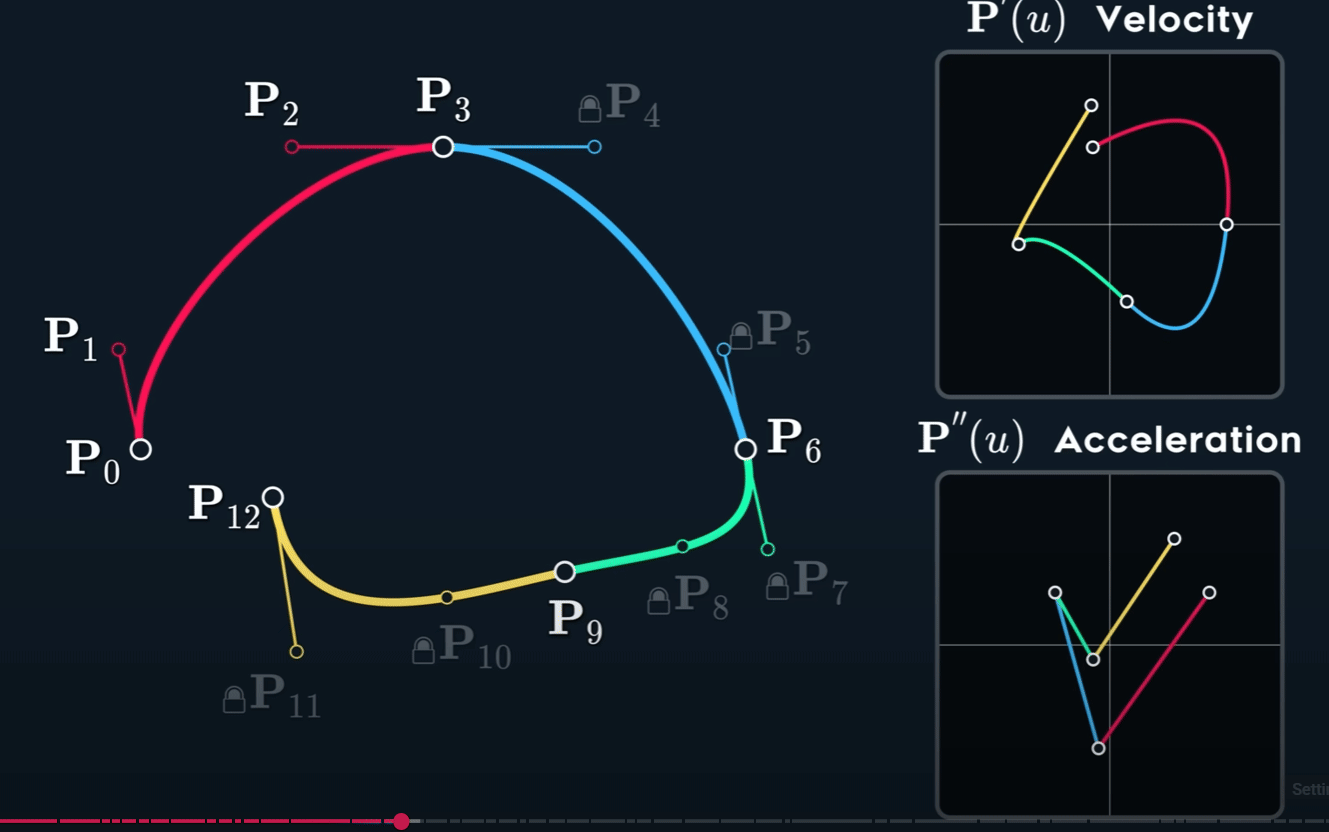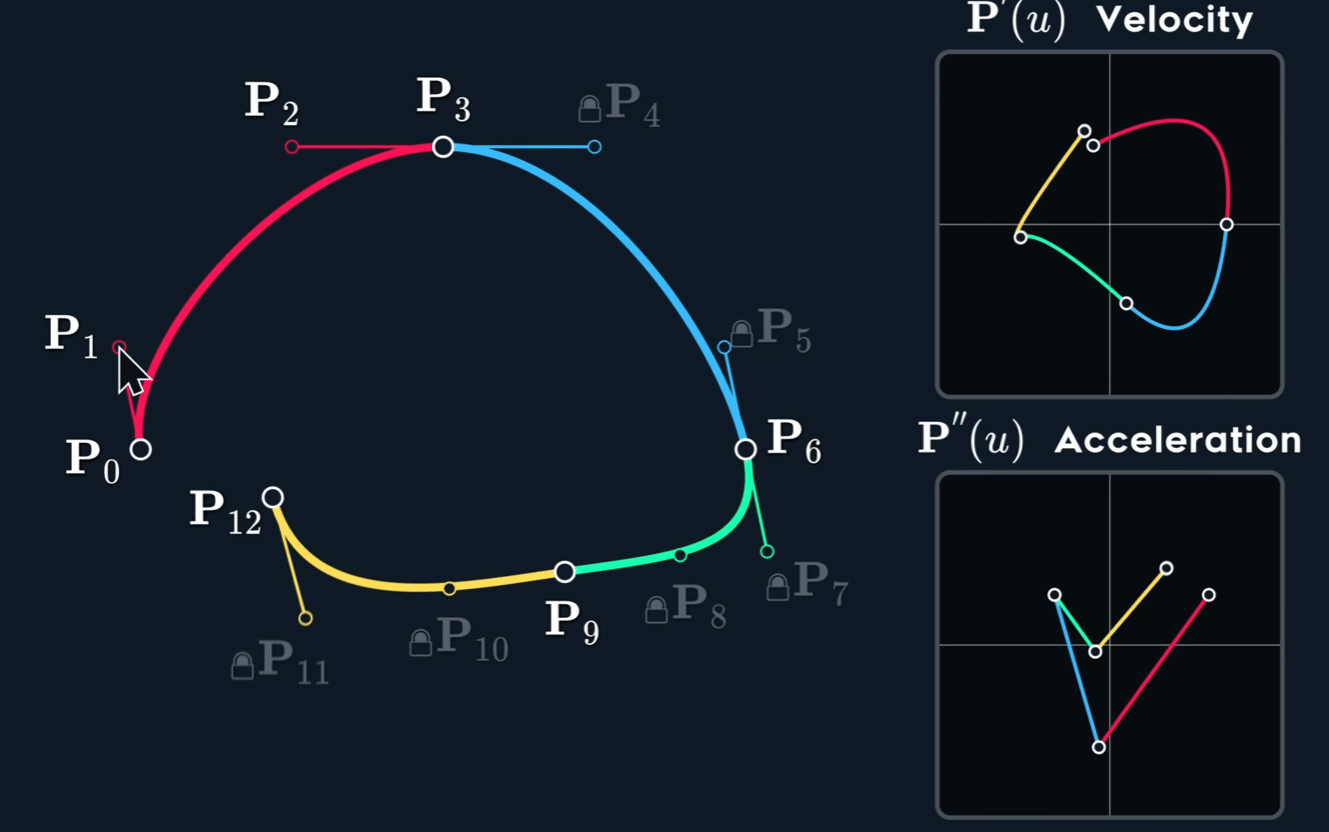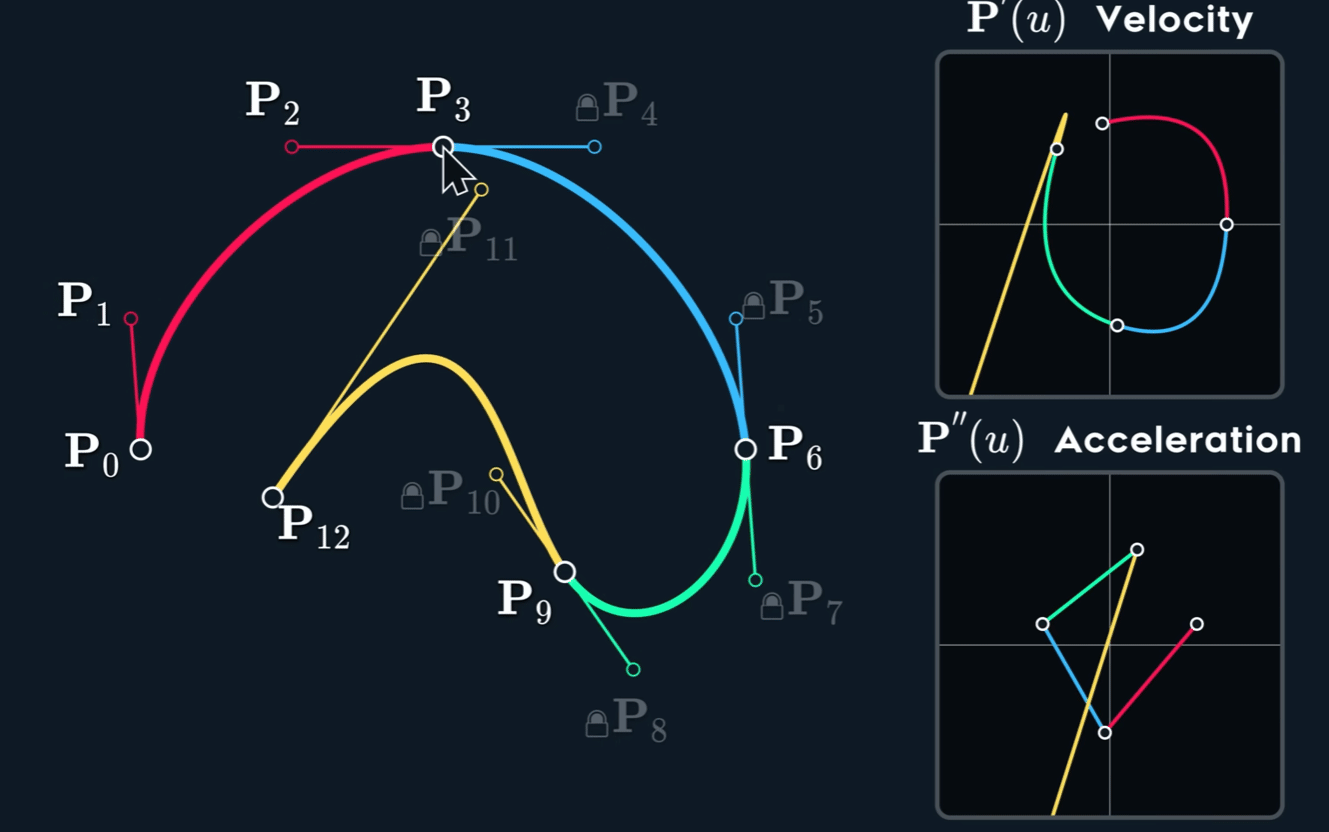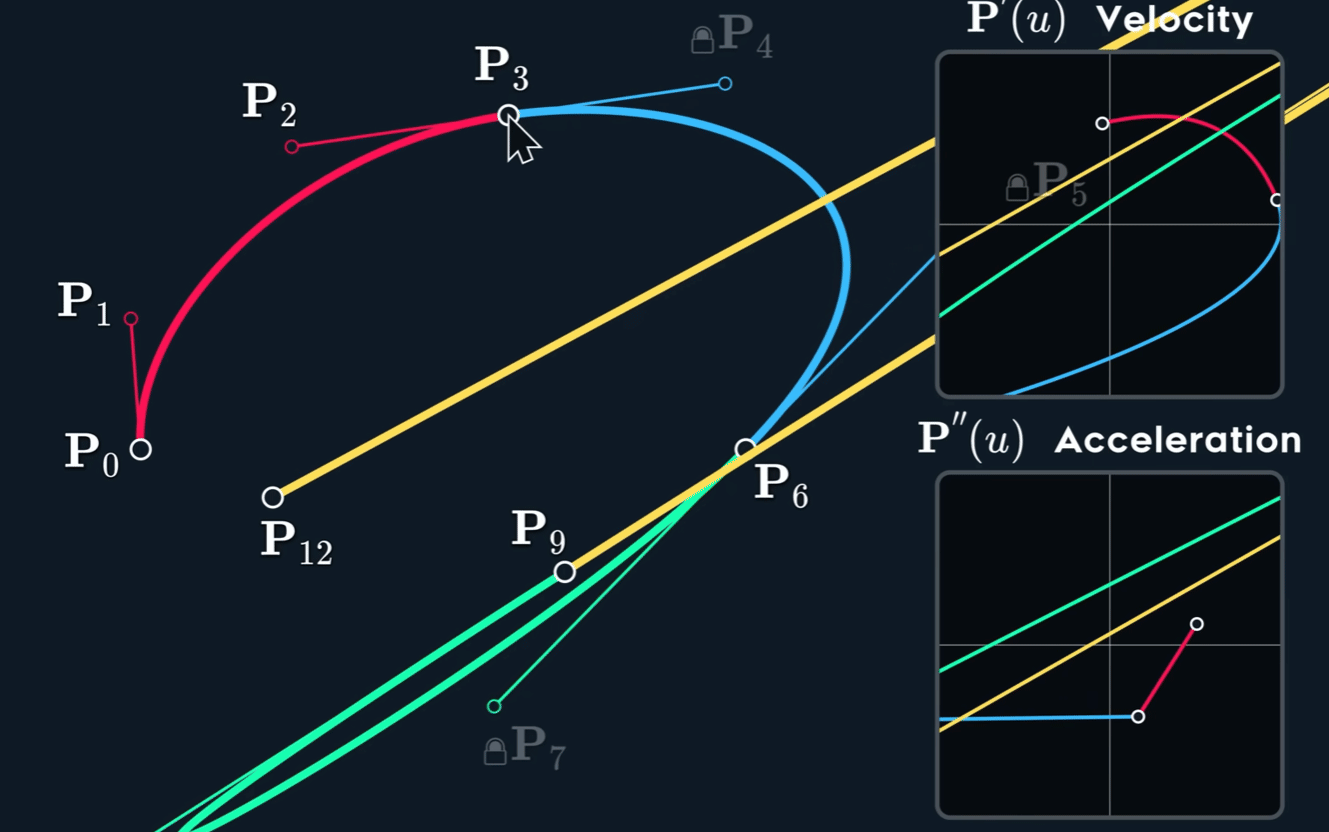
对于多段贝塞尔曲线构成的spline,保证$C^2$时,很多控制点的位置都已经被完全决定,控制能力变弱了,并且, 微小的控制会导致后面剧烈的变化。
Geometric Continuity
$A(t)$ and $B(t)$ are
$G^n$ ccontinuous if a function $g(t)$ exists so that $A(t)$ and $B(g(t))$ are $C^{n}$ continuous
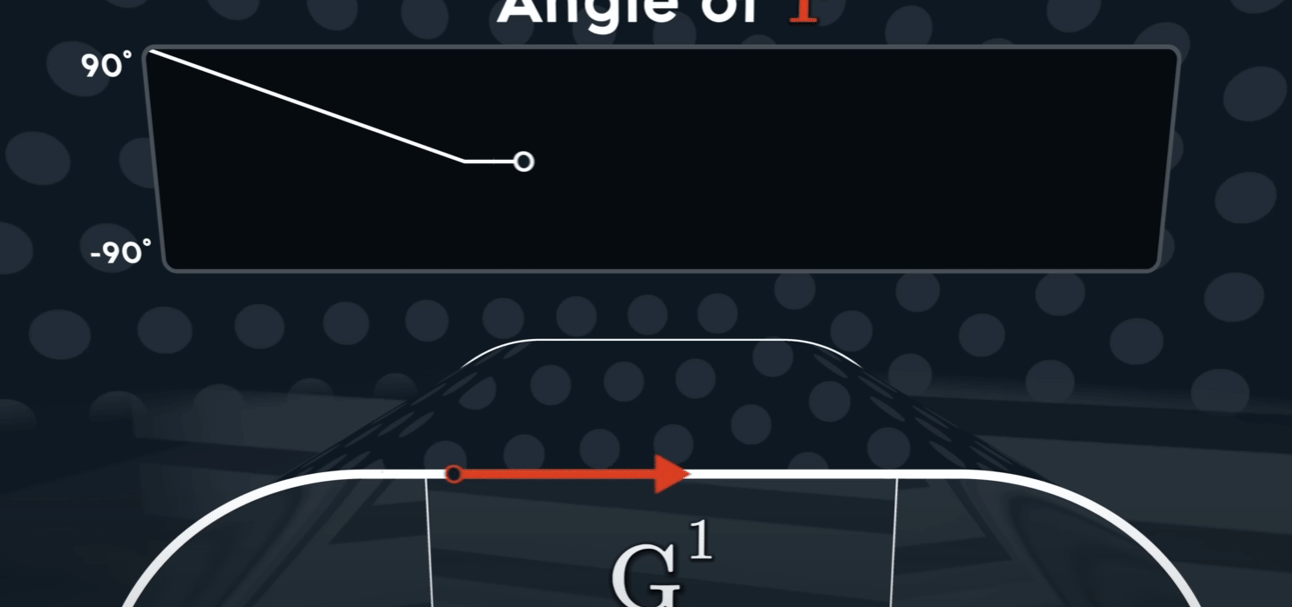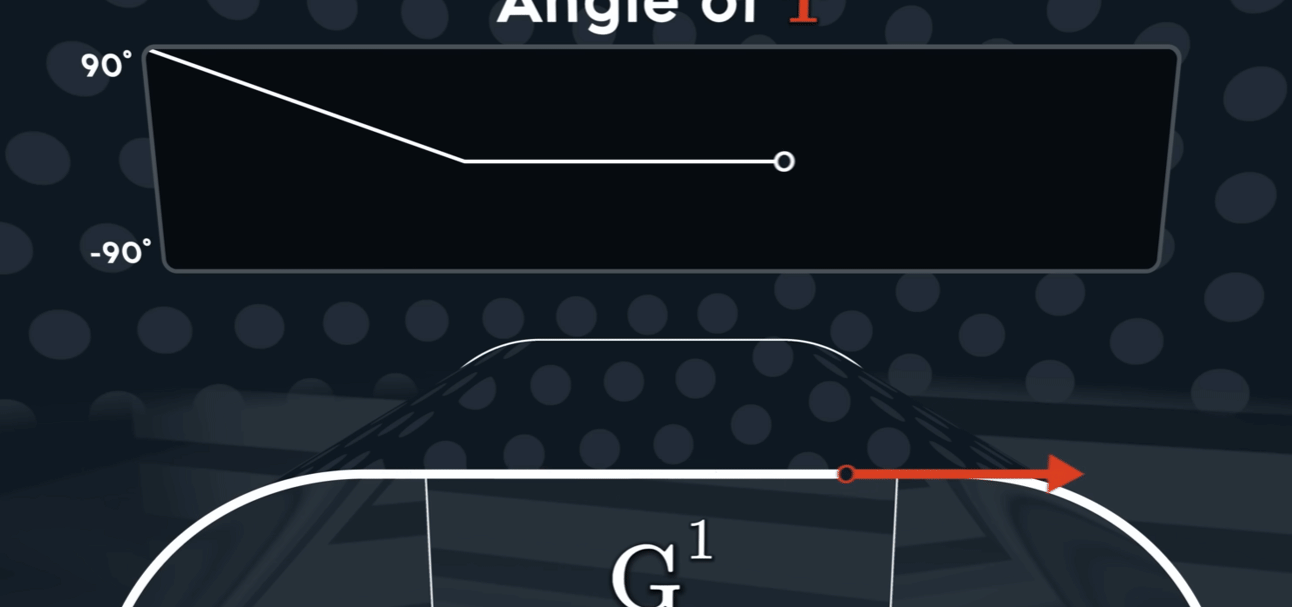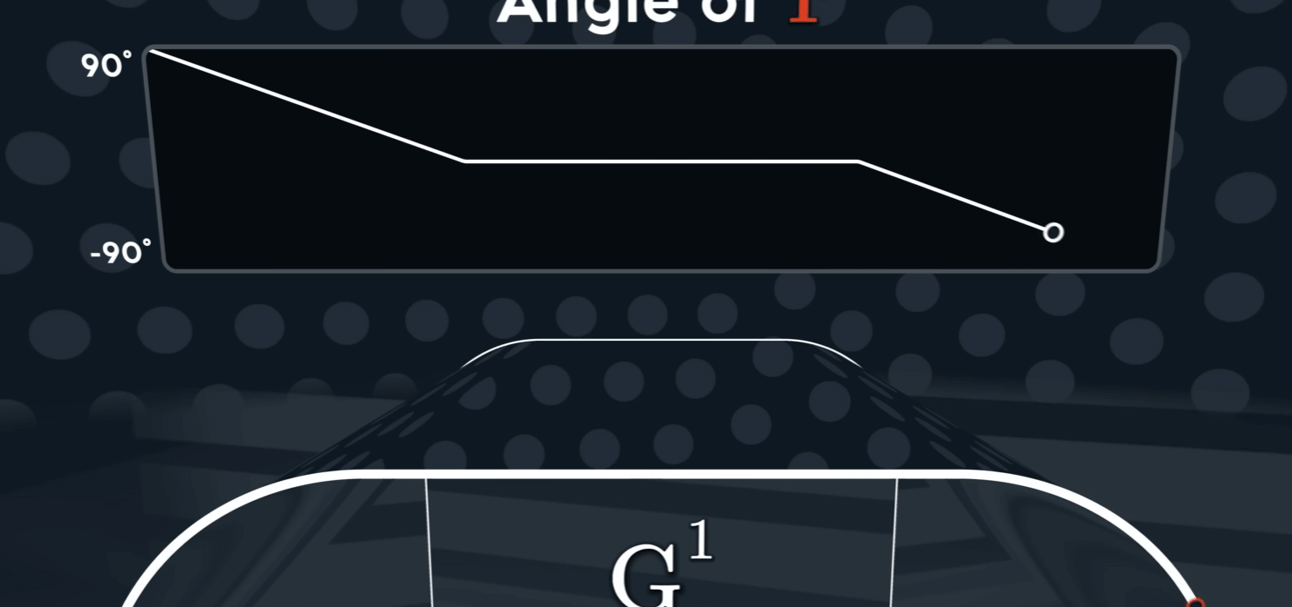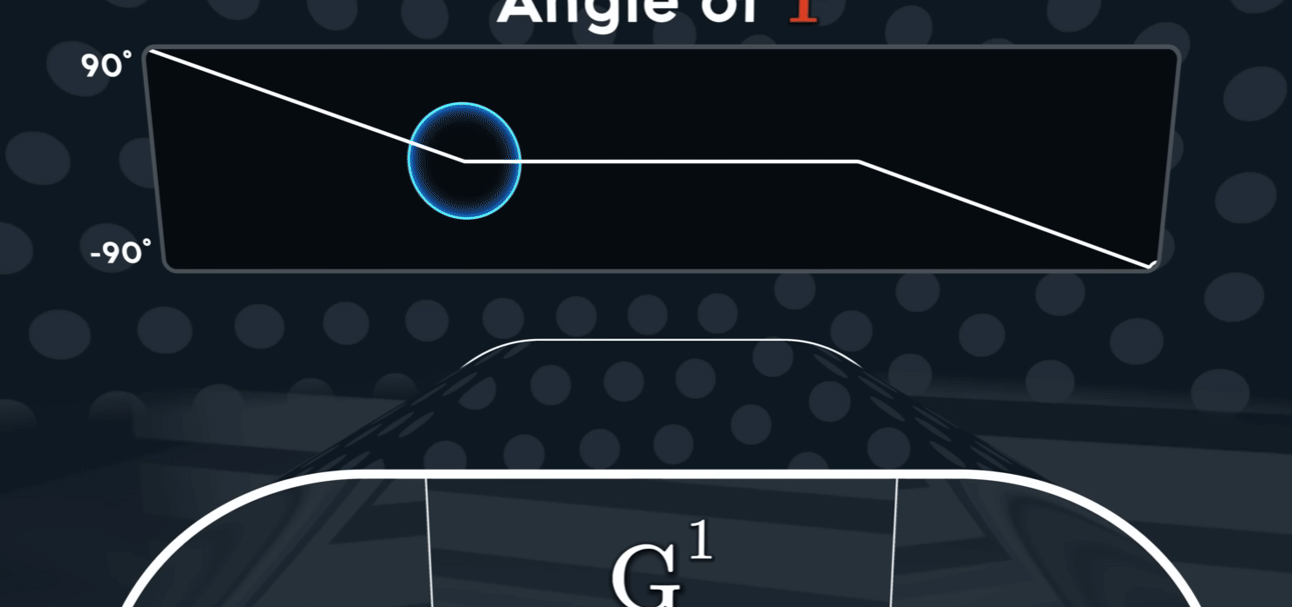
$G^{1}$
切线连续性通常用 G¹ 连续性 (Geometric Continuity, first-order) 来表示。为了让两条曲线在连接点处达到 G¹ 连续,必须满足以下两个条件:
G⁰ 位置连续性 (Positional Continuity): 两条曲线的端点必须在连接点处重合。也就是说,它们必须接触。
切线方向相同: 在连接点处,两条曲线的切线向量必须指向相同的方向(或者完全相反的方向,但在实际应用中通常要求方向一致)。这意味着两条曲线在该点的变化趋势是一致的。
值得注意的是,G¹ 连续性只要求切线的方向相同,而不要求切线向量的大小(即参数导数的大小)也相同。如果切线向量的大小和方向都相同,那么就达到了更高级别的 $C^1$ 参数连续性 (Parametric Continuity, first-order)。 $C^1$ 连续性是比 G¹ 更严格的条件
满足 $G^{1}$ 时,有
$$
b_4 = b_3 + (b_3 - b_2) \beta
$$
即,共线同向,但不要求大小相同。
在曲面上,我们可以注意到反光有条缝
Curvature $k$
$$ \kappa = \frac{\begin{vmatrix} P'_{x} & P''_{x} \\\\ P'_{y} & P''_{y} \end{vmatrix}}{{\Vert \mathbf{P}' \Vert}^3} $$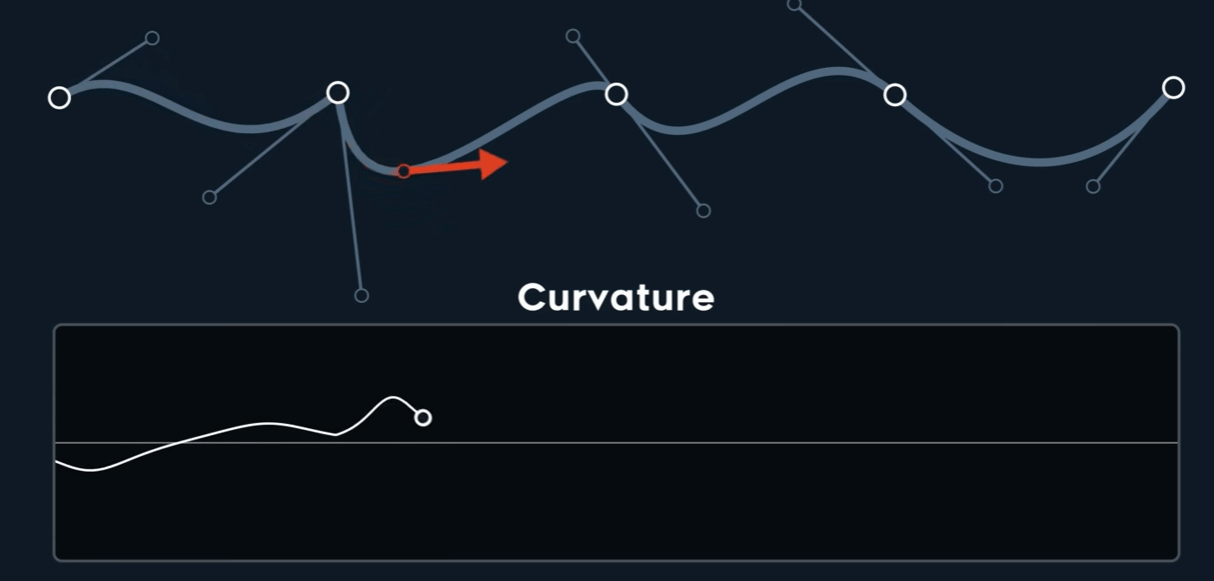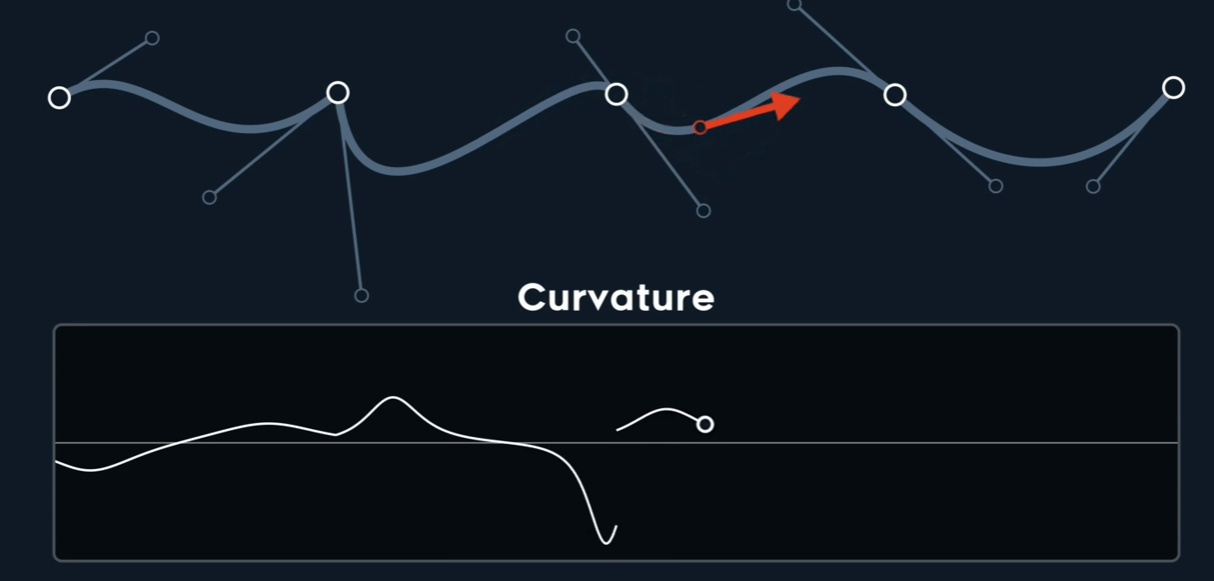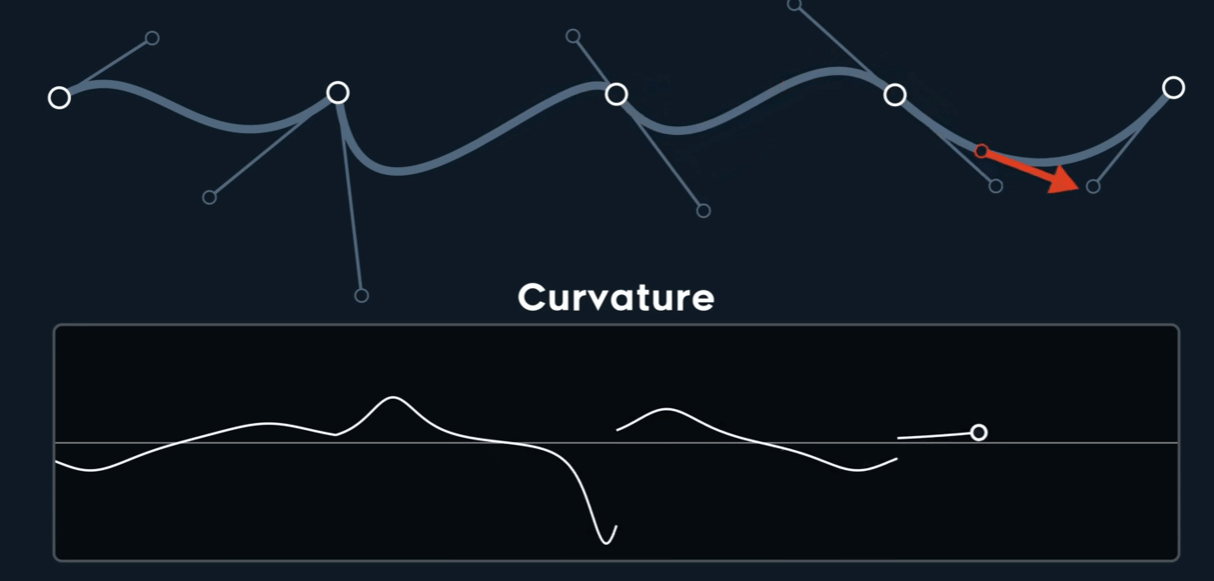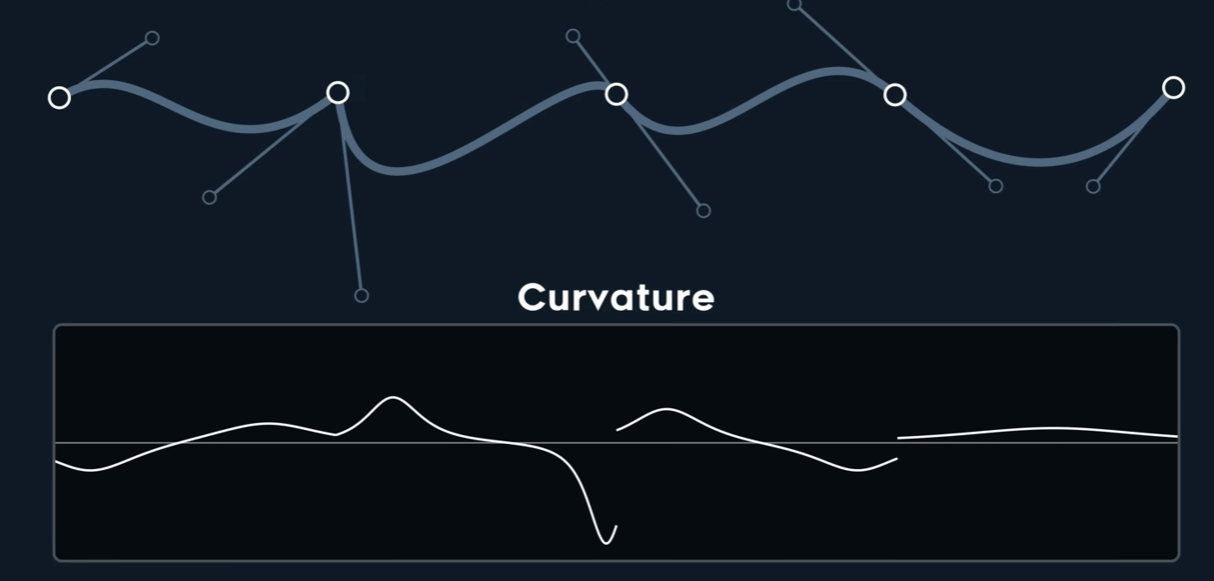
仅仅$C^{0}$时,也可能是Curvature连续的,而$C^{1}$时,未必连续。
$G^{2}$ 连续性
$$
\mathbf{P}_5 = \mathbf{P}_3 + (\mathbf{P}_3 - \mathbf{P}_2)(2\beta_1 + \beta_1^2 + \beta_2/2) + (\mathbf{P}_1 - \mathbf{P}_2)\beta_1^2
$$
$\mathbf{P}_5$ 被上述控制点与参数共同决定。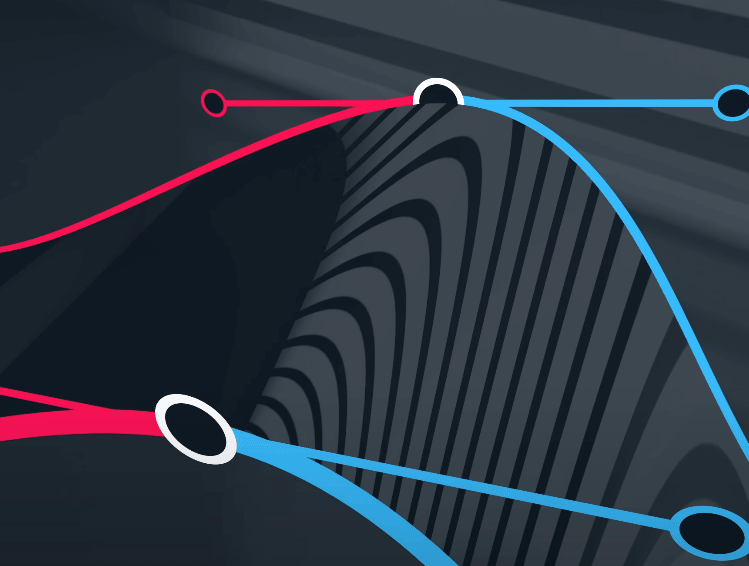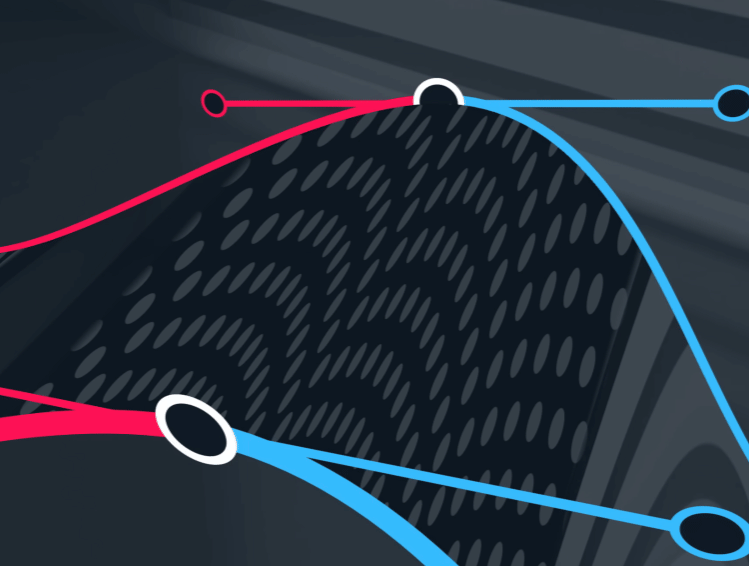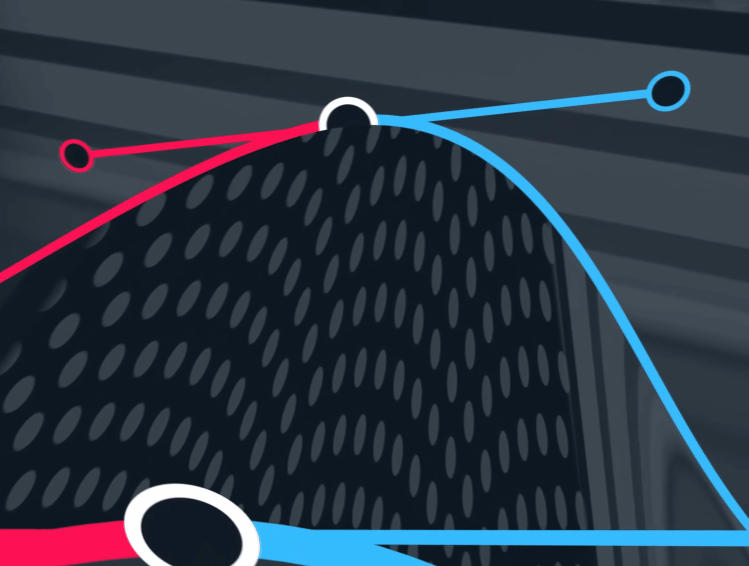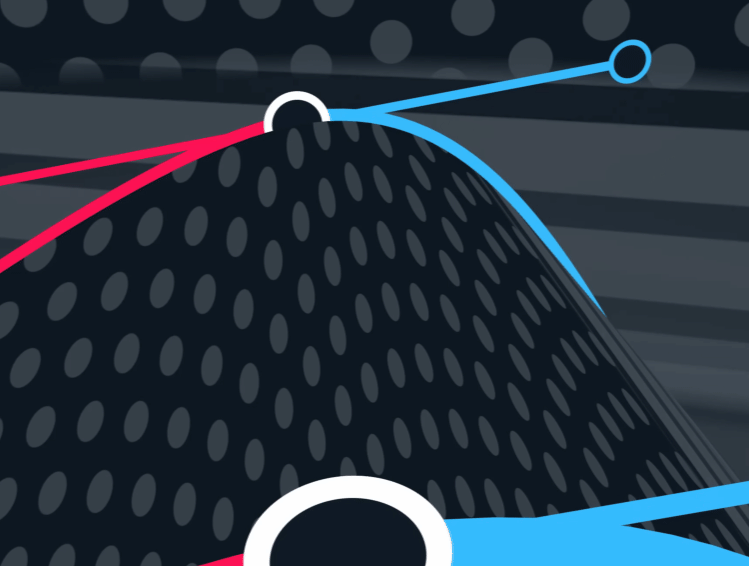
$G^{2}$ 以及以上被称为A级面
*as long as the curves are regular
Hermite Curves
贝塞尔曲线利用四个控制点来构造,而Hermite曲线由两个端点和端点的速度。即
$$
P(0) = P_0 \\
P(1) = P_1 \\
P’(0) = \mathbf{v}_0 \\
P’(1) = \mathbf{v}_1
$$
通过上述关系求解
$$
P(t) = at^3 + bt^2 + ct + d
$$
得到
$$
\mathbf{P}(t) =
\begin{bmatrix}
1 & t & t^2 & t^3
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
-3 & -2 & 3 & -1 \\
2 & 1 & -2 & 1
\end{bmatrix}
\begin{bmatrix}
\mathbf{P}_0 \\
\mathbf{v}_0 \\
\mathbf{P}_1 \\
\mathbf{v}_1
\end{bmatrix}
$$
通过设置连接点处切向量相等,可以方便地实现$C^1$
Hermite to Bezier:
$$
B_0 = P_0 \\
B_1 = P_0 + v_0/3 \\
B_2 = P_1 - v_1/3 \\
B_3 = P_1
$$
Cardinal Spline
从此处开始$ \mathbf{P}_0$,$ \mathbf{P}_1$,$ \mathbf{P}_2$,$ \mathbf{P}_3$ 指的是spline上的相邻四个joints点
如何串联一系列给定的点呢?
我们可以采用一种类似Hermite的方法,我们计算一个joint相邻两点的位移,并以此作为此点的速度
但首尾两点并没有被穿进去,我们可以将原第二个点关于首个joint对称过去。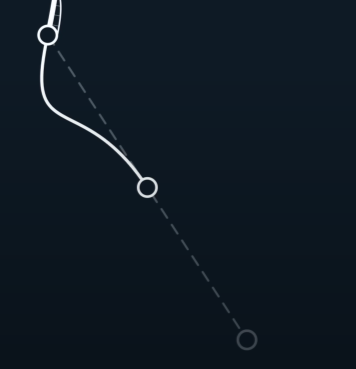
但是这样得到的曲线看起来有些呆板。出现了长段的较为平坦的线条,我们可以引入一个 Scale 参数 $s$ 来缩放我们的速度。当$s$接近于0的时候,也就退化成了线性spline
$$
\mathbf{P}(t) =
\begin{bmatrix}
1 & t & t^2 & t^3
\end{bmatrix}
\begin{bmatrix}
0 & 1 & 0 & 0 \\
-s & 0 & s & 0 \\
2s & s-3 & 3-2s & -s \\
-s & 2-s & s-2 & s
\end{bmatrix}
\begin{bmatrix}
\mathbf{P}_0 \\
\mathbf{P}_1 \\
\mathbf{P}_2 \\
\mathbf{P}_3
\end{bmatrix}
$$
当$s = 0.5$时,我们有
Catmull-Rom Spline
- Interpolating every point!
- $C^1$ continuous, not $C^{2}$
- No need to specify tangents
$$
\mathbf{P}(t) = \begin{bmatrix} 1 & t & t^2 & t^3 \end{bmatrix} \frac{1}{2} \begin{bmatrix} 0 & 2 & 0 & 0 \\ -1 & 0 & 1 & 0 \\ 2 & -5 & 4 & -1 \\ -1 & 3 & -3 & 1 \end{bmatrix} \begin{bmatrix} \mathbf{P}_0 \\ \mathbf{P}_1 \\ \mathbf{P}_2 \\ \mathbf{P}_3 \end{bmatrix}
$$
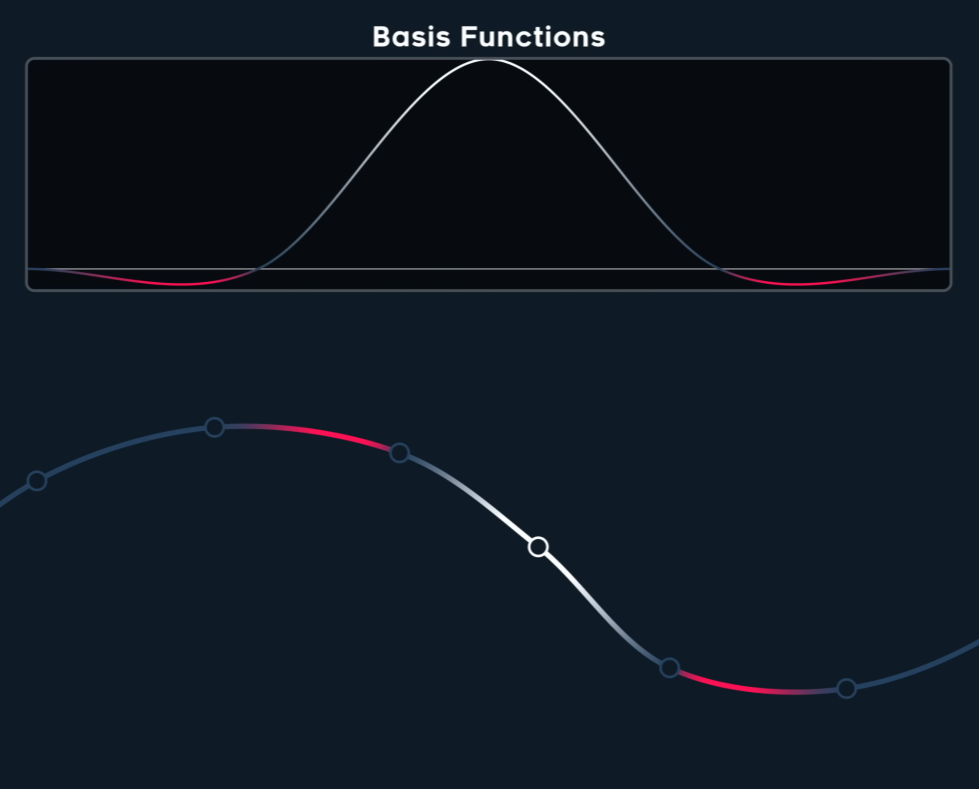
B-Spline(Basis-Spline)
那么,有没有一种构造Spline的方式,使之可以满足$C^2$呢?也就是说,我们要对这个求解:
$$
\mathbf{P}(t) =
\begin{bmatrix}
1 & t & t^2 & t^3
\end{bmatrix}
\begin{bmatrix}
\textcolor{red}{c_0} & \textcolor{cyan}{c_1} & \textcolor{green}{c_2} & \textcolor{orange}{c_3} \\
\textcolor{red}{c_4} & \textcolor{cyan}{c_5} & \textcolor{green}{c_6} & \textcolor{orange}{c_7} \\
\textcolor{red}{c_8} & \textcolor{cyan}{c_9} & \textcolor{green}{c_{10}} & \textcolor{orange}{c_{11}} \\
\textcolor{red}{c_{12}} & \textcolor{cyan}{c_{13}} & \textcolor{green}{c_{14}} & \textcolor{orange}{c_{15}}
\end{bmatrix}
\begin{bmatrix}
\textcolor{red}{\mathbf{P}_0} \\
\textcolor{cyan}{\mathbf{P}_1} \\
\textcolor{green}{\mathbf{P}_2} \\
\textcolor{orange}{\mathbf{P}_3}
\end{bmatrix}
$$
$$
\begin{gather}
\textcolor{red}{B_0(1) = 0} \tag{1} \
\textcolor{red}{B’{0}(1) = 0} \tag{2} \
\textcolor{red}{B’’{0}(1) = 0} \tag{3} \
\textcolor{red}{B_0(0)} = \textcolor{cyan}{B_1(1)} \tag{4} \
\textcolor{red}{B’{0}(0)} = \textcolor{cyan}{B’{1}(1)} \tag{5} \
\textcolor{red}{B’’{0}(0)} = \textcolor{cyan}{B’’{1}(1)} \tag{6} \
\textcolor{cyan}{B_1(0)} = \textcolor{green}{B_2(1)} \tag{7} \
\textcolor{cyan}{B’{1}(0)} = \textcolor{green}{B’{2}(1)} \tag{8} \
\textcolor{cyan}{B’’{1}(0)} = \textcolor{green}{B’’{2}(1)} \tag{9} \
\textcolor{green}{B_2(0)} = \textcolor{orange}{B_3(1)} \tag{10} \
\textcolor{green}{B’{2}(0)} = \textcolor{orange}{B’{3}(1)} \tag{11} \
\textcolor{green}{B’’{2}(0)} = \textcolor{orange}{B’’{3}(1)} \tag{12} \
\textcolor{orange}{B_3(0) = 0} \tag{13} \
\textcolor{orange}{B’{3}(0) = 0} \tag{14} \
\textcolor{orange}{B’’{3}(0) = 0} \tag{15} \
\textcolor{red}{B_0(t)} + \textcolor{cyan}{B_1(t)} + \textcolor{green}{B_2(t)} + \textcolor{orange}{B_3(t)} = 1 \tag{16}
\end{gather}
$$

$$
\mathbf{P}(t) =
\begin{bmatrix}
1 & t & t^2 & t^3
\end{bmatrix}
\frac{1}{6}
\begin{bmatrix}
1 & 4 & 1 & 0 \
-3 & 0 & 3 & 0 \
3 & -6 & 3 & 0 \
-1 & 3 & -3 & 1
\end{bmatrix}
\begin{bmatrix}
\textcolor{red}{\mathbf{P}_0} \
\textcolor{cyan}{\mathbf{P}_1} \
\textcolor{green}{\mathbf{P}_2} \
\textcolor{orange}{\mathbf{P}_3}
\end{bmatrix}
$$
- Not interpolating
- $C^2$ continuous! $G ^ 2$
B 样条的递推定义
refer to B样条的定义de boor-cox公式的理解
数学定义:
$$
P(t) = \sum_{i=0}^{n} P_i F_{i,k}(t) \qquad t \in [t_{k-1}, t_{n+1}]
$$
$k$ 是 B 样条的次数
$n$ 是控制点的最大索引,如果有$P_{i}, (i = 0, 1, …, n)$共 $n + 1$个控制点,那么最大索引就是$n$
$i$ 是这些控制点的序号
de Boor-Cox 递推定义,只与 t 有关
基函数的递推:
$$
\left{
\begin{aligned}
& F_{i,0}(t) =
\begin{cases}
1, & t_i \le t < t_{i+1} \
0, & \text{其他}
\end{cases}
\[2ex]
& F_{i,k}(t) = \frac{t-t_i}{t_{i+k}-t_i} F_{i,k-1}(t) + \frac{t_{i+k+1}-t}{t_{i+k+1}-t_{i+1}} F_{i+1,k-1}(t)
\[2ex]
& \text{约定 } \frac{0}{0} = 0
\end{aligned}
\right.
$$
$i$ 是基函数的编号,每个$P_i$都有一个权重函数,也就是基函数。
$i$ 也是向量节点 $T$ 中节点的索引。基函数$F_{i,k}(t)$的具体形状,它在时间轴上的起点和终点,完全是由节点向量$T = [t_0, t_1, t_2, … ]$ 决定的。$i$ 告诉我们,基函数 $F_{i,k}(t)$ 在 $[t_i, t_{i+k+1}]$ 是不为零的。
控制点的递推:
$$
\begin{equation*}
\mathbf{P}{i,r}(t) = (1 - \alpha{i,r}) \mathbf{P}{i-1, r-1}(t) + \alpha{i,r} \mathbf{P}_{i, r-1}(t) \tag{}
\end{equation*}
$$
$$
\alpha_{i,r} = \frac{t - t_i}{t_{i+k+1-r} - t_i}
$$
$k$ 是 B 样条的次数,那么这个样条的阶数是$k+1$, 一段就有$k+1$个控制点
$r$ 是计算的轮数,$r$从1走到$k$
我们把所有的(不仅是某一段的), 共(n + 1)个控制点记作 $P_{i}, (i = 0, 1, …, n)$ ,有 n + k +2 ($节点数 = 总控制点数 + 次数 + 1$) 个节点矢量 $T = [t_0, t_1, … t_{n + k + 1}]$
例如,5 个控制点,3次的B样条曲线,由于一段是由4个控制点决定的,那么就有(5-3 = )2个线段,1个joint
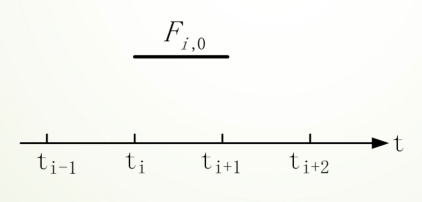
对于零次B样条:
其基函数可以直接得到
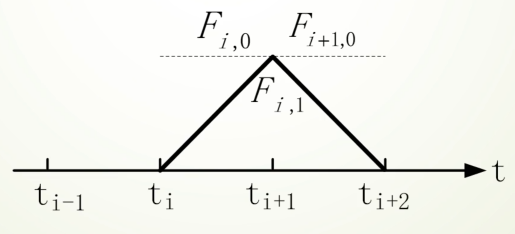
对于一次B样条:
$$
F_{i,1}(t) = \frac{t - t_i}{t_{i+1} - t_i} F_{i,0}(t) + \frac{t_{i+2} - t}{t_{i+2} - t_{i+1}} F_{i+1,0}(t)
$$
$$
F_{i+1,0}(t) =
\begin{cases}
1, & \text{若 } t_{i+1} \le t < t_{i+2} \[1.5ex]
0, & \text{其他}
\end{cases}
$$
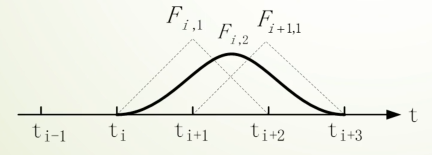
对于二次 B 样条:
$$
F_{i,2}(t) = \frac{t-t_i}{t_{i+2}-t_i} F_{i,1}(t) + \frac{t_{i+3}-t}{t_{i+3}-t_{i+1}} F_{i+1,1}(t)
$$
$$
F_{i+1,1}(t) =
\begin{cases}
\frac{t-t_{i+1}}{t_{i+2}-t_{i+1}}, & \text{若 } t_{i+1} \le t < t_{i+2} \[2ex]
\frac{t_{i+3}-t}{t_{i+3}-t_{i+2}}, & \text{若 } t_{i+2} \le t < t_{i+3} \[2ex]
0, & \text{其他}
\end{cases}
$$
对于三次 B 样条:
$$
F_{i,3}(t) = \frac{t - t_i}{t_{i+3} - t_i} F_{i,2}(t) + \frac{t_{i+4} - t}{t_{i+4} - t_{i+1}} F_{i+1,2}(t)
$$
$$
F_{i+1,2}(t) =
\begin{cases}
\frac{t - t_{i+1}}{t_{i+3} - t_{i+1}} \cdot \frac{t - t_{i+1}}{t_{i+2} - t_{i+1}}, & \text{若 } t_{i+1} \le t < t_{i+2} \[3ex]
\frac{t-t_{i+1}}{t_{i+3}-t_{i+1}} \cdot \frac{t_{i+3}-t}{t_{i+3}-t_{i+2}} + \frac{t_{i+4}-t}{t_{i+4}-t_{i+2}} \cdot \frac{t-t_{i+2}}{t_{i+3}-t_{i+2}}, & \text{若 } t_{i+2} \le t < t_{i+3} \[3ex]
\frac{(t_{i+4}-t)^2}{(t_{i+4}-t_{i+2})(t_{i+4}-t_{i+3})}, & \text{若 } t_{i+3} \le t < t_{i+4} \[3ex]
0, & \text{其他}
\end{cases}
$$
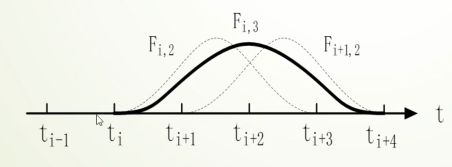
例
三次 B 样条, 控制点为$P_0 = (30, 0)$, $P_1 = (60, 10)$, $P_2 = (80, 30)$, $P_3 = (90, 60)$, $P_4 = (90, 90)$,节点向量(Knot Vector): $T = [t_0, t_1, t_2, t_3,t_4,t_5,t_6,t_7, t_8] = [0,0,0,0,0.5, 1,1,1,1]$
求曲线上一点 $P(\frac{1}{4})$ 的值
首先观察这个点在哪个区间上,由于$t_3 = 0 < \frac{1}{4} < t_4 = 0.5$, 那么这个区间的索引是 $i = 3$
在区间$[t_i, t_{i+1})$内, 对于$k$次B样条,需要用到$k + 1$个控制点,这些点的索引是$P_{i-k}$, $P_{i-k +1}, … P_{i}$
那么,在区间$[t_3, t_{4})$ 内,对于3次B样条,需要用到4个控制点,这些点的索引是$P_0, P_1, P_2, P_3$
对于 k 次B样条,需要经行 k 轮运算,每一轮都使用上一轮计算出的点进行插值。
回顾数学定义:
$$
P(t) = \sum_{i=0}^{n} P_i F_{i,k}(t)
$$
$$
P(\frac{1}{4}) = \sum_{i=0}^{3} P_i F_{i,3}(\frac{1}{4}) \
P(\frac{1}{4}) = P_0F_{0,3}(\frac{1}{4}) + P_1 F_{1,3}(\frac{1}{4}) + P_2 F_{2,3}(\frac{1}{4}) + P_3F_{3,3}(\frac{1}{4})
$$
据此,利用上述的关于$F_{i,k}$的递推关系,我们可以算出各个$F_{i,k}$ 的值,进而$P(\frac{1}{4})$的值。不过,基于$F_{i,k}$的递推关系,我们可以找到一些最终值和控制点的关系:
$$
\begin{equation*}
\mathbf{P}{i,r}(t) = (1 - \alpha{i,r}) \mathbf{P}{i-1, r-1}(t) + \alpha{i,r} \mathbf{P}_{i, r-1}(t) \tag{}
\end{equation*}
$$
$$
\alpha_{i,r} = \frac{t - t_i}{t_{i+k+1-r} - t_i}
$$
第一轮计算,也就是 $r = 1$:
计算 $P_{1,1}$ ,由 $P_{0,0}$ 和 $P_{1,0}$ 插值得到
权重 $\alpha_{1,1} = \frac{t - t_1}{t_{1+3+1-1} - t_1} = \frac{0.25 - t_1}{t_4 - t_1} = \frac{0.25 - 0}{0.5 - 0} = 0.5$
$P_{1,1} = (1 - 0.5)P_{0,0} + 0.5 \cdot P_{1,0} = 0.5(30,0) + 0.5(60,10) = (15,0) + (30,5) = (45, 5)$
计算 $P_{2,1}$ (由 $P_{1,0}$ 和 $P_{2,0}$ 插值得到):
- 权重 $\alpha_{2,1} = \frac{t - t_2}{t_{2+3+1-1} - t_2} = \frac{0.25 - t_2}{t_5 - t_2} = \frac{0.25 - 0}{1 - 0} = 0.25$
- $P_{2,1} = (1 - 0.25)P_{1,0} + 0.25 \cdot P_{2,0} = 0.75(60,10) + 0.25(80,30) = (45, 7.5) + (20, 7.5) = (65, 15)$
计算 $P_{3,1}$ (由 $P_{2,0}$ 和 $P_{3,0}$ 插值得到):
- 权重 $\alpha_{3,1} = \frac{t - t_3}{t_{3+3+1-1} - t_3} = \frac{0.25 - t_3}{t_6 - t_3} = \frac{0.25 - 0}{1 - 0} = 0.25$
- $P_{3,1} = (1 - 0.25)P_{2,0} + 0.25 \cdot P_{3,0} = 0.75(80,30) + 0.25(90,60) = (60, 22.5) + (22.5, 15) = (82.5, 37.5)$
第二轮计算,也就是 $r = 2$:
计算 $P_{2,2}$ (由 $P_{1,1}$ 和 $P_{2,1}$ 插值得到):
权重 $\alpha_{2,2} = \frac{t - t_2}{t_{2+3+1-2} - t_2} = \frac{0.25 - t_2}{t_4 - t_2} = \frac{0.25 - 0}{0.5 - 0} = 0.5$
$P_{2,2} = (1 - 0.5)P_{1,1} + 0.5 \cdot P_{2,1} = 0.5(45,5) + 0.5(65,15) = (22.5, 2.5) + (32.5, 7.5) = (55, 10)$
计算 $P_{3,2}$ (由 $P_{2,1}$ 和 $P_{3,1}$ 插值得到):
权重 $\alpha_{3,2} = \frac{t - t_3}{t_{3+3+1-2} - t_3} = \frac{0.25 - t_3}{t_5 - t_3} = \frac{0.25 - 0}{1 - 0} = 0.25$
$P_{3,2} = (1 - 0.25)P_{2,1} + 0.25 \cdot P_{3,1} = 0.75(65,15) + 0.25(82.5, 37.5) = (48.75, 11.25) + (20.625, 9.375) = (69.375, 20.625)$
第三轮计算 ($r = 3$),最终结果
计算 $P_{3,3}$ (由 $P_{2,2}$ 和 $P_{3,2}$ 插值得到):
权重 $\alpha_{3,3} = \frac{t - t_3}{t_{3+3+1-3} - t_3} = \frac{0.25 - t_3}{t_4 - t_3} = \frac{0.25 - 0}{0.5 - 0} = 0.5$
$P_{3,3} = (1 - 0.5)P_{2,2} + 0.5 \cdot P_{3,2} = 0.5(55,10) + 0.5(69.375, 20.625)$
$P_{3,3} = (27.5, 5) + (34.6875, 10.3125) = (62.1875, 15.3125)$
Trajectory
$$
\begin{bmatrix} 1 & 0 & 0 & 0 \ 0 & 1! & 0 & 0 \ 0 & 0 & 1/2! & 0 \ 0 & 0 & 0 & 1/3! \end{bmatrix} \begin{bmatrix} \mathbf{p}_0 \ \mathbf{v}_0 \ \mathbf{g}_0 \ \mathbf{j}_0 \end{bmatrix}
$$
$$
\mathbf{P}(t) = \begin{bmatrix} 1 & t & t^2 & t^3 \end{bmatrix} \begin{bmatrix} \mathbf{p}_0 \ \mathbf{v}_0 \ \frac{1}{2}\mathbf{g}_0 \ \frac{1}{6}\mathbf{j}_0 \end{bmatrix} = \mathbf{p}_0 \cdot 1 + \mathbf{v}_0 \cdot t + \left(\frac{1}{2}\mathbf{g}_0\right) \cdot t^2 + \left(\frac{1}{6}\mathbf{j}_0\right) \cdot t^3
$$
Conclusion
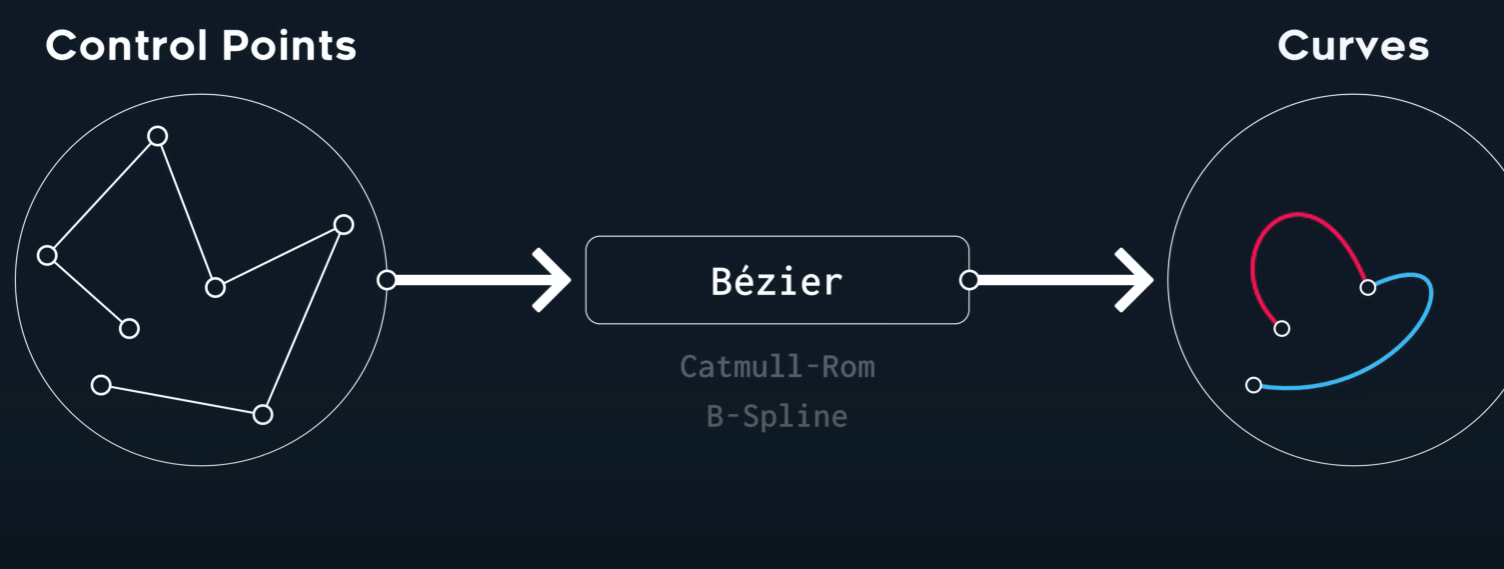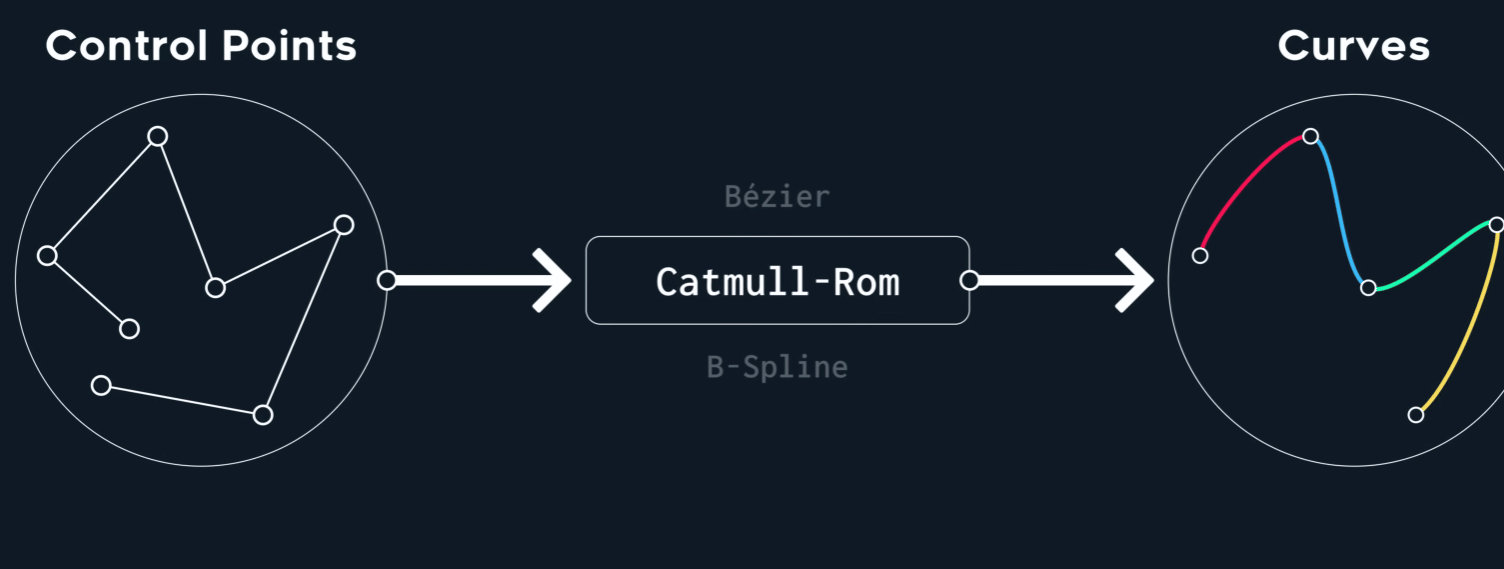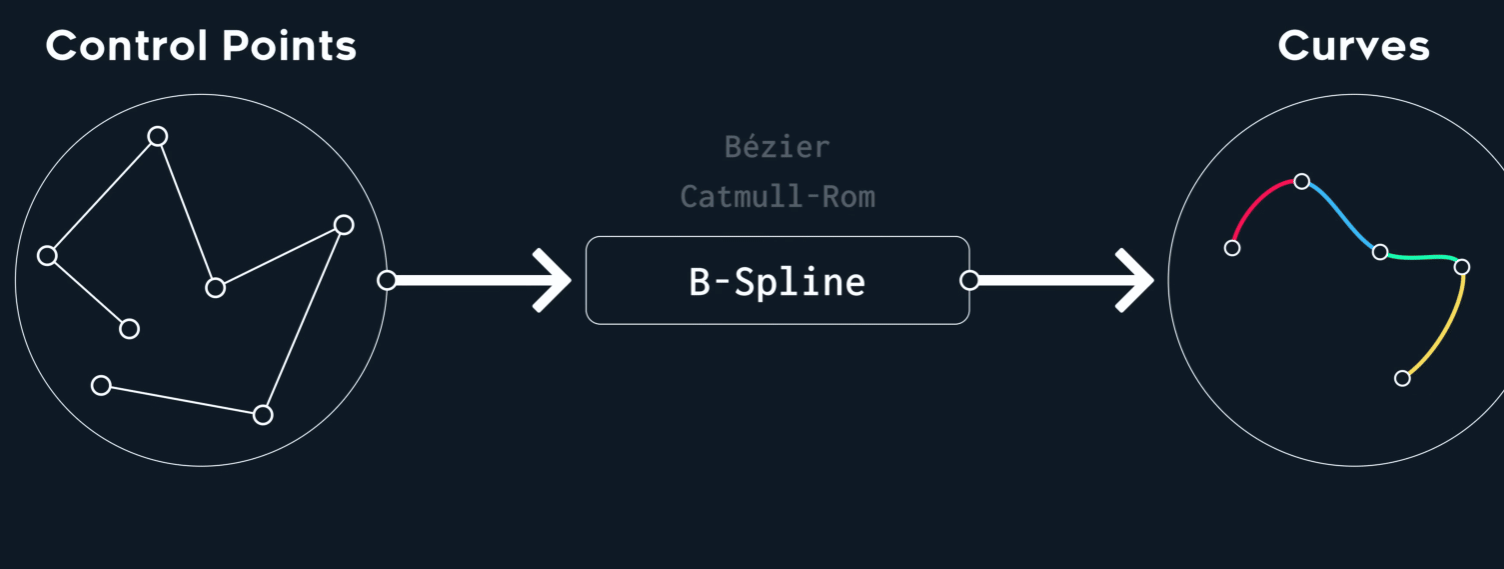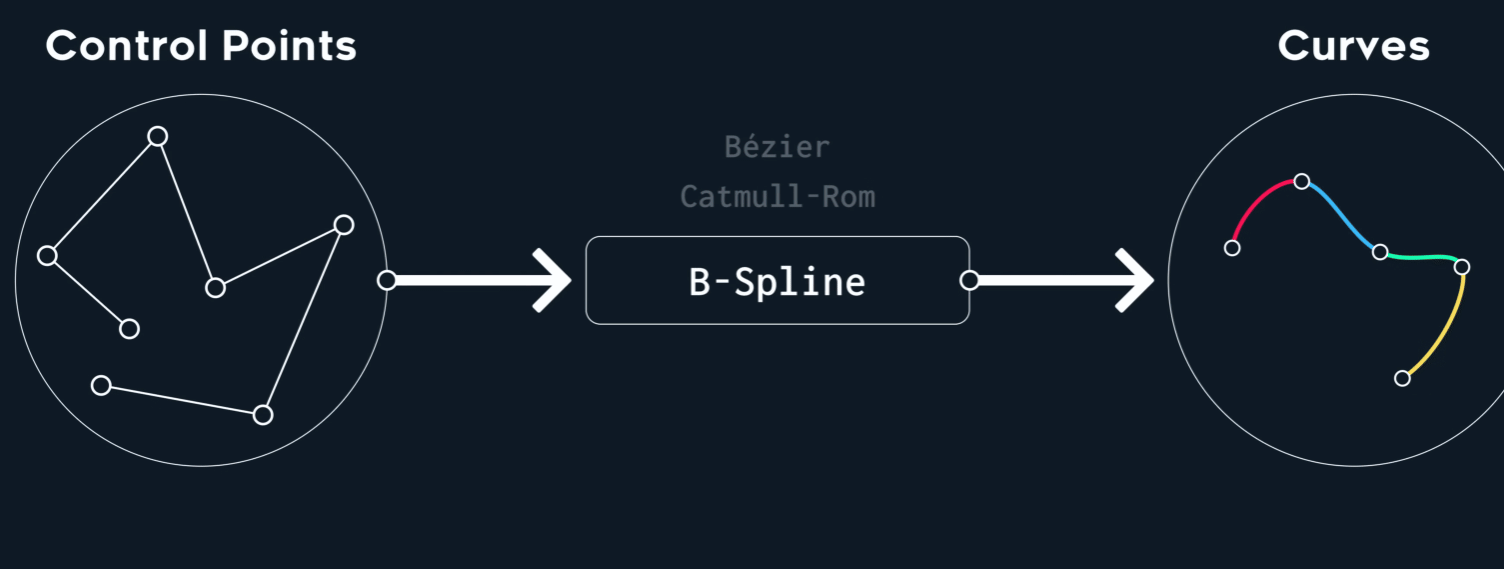
| Deg. | Cont. | Tangents | Interpol. | Use cases | |
|---|---|---|---|---|---|
| Bézier | 3 | C⁰/C¹ | manual | some | shapes, fonts & vector graphics |
| Hermite | 3 | C⁰/C¹ | explicit | all | animation, physics sim & interpolation |
| Catmull-Rom | 3 | C¹ | auto | all | animation & path smoothing |
| B-Spline | 3 | C² | auto | none | curvature-sensitive shapes & animations, such as camera paths |
| Linear | 1 | C⁰ | auto | all | dense data & interpolation where smoothness doesn’t matter |
Handling Non-Uniform Time in Splines
目前讨论的是最经典的情况,即每个曲线段的“时长”都是1个单位(称之为**参数化均匀 (Uniform Parameterization)**)。
当每个曲线段的实际时间或“长度”不同时(参数化非均匀, Non-Uniform Parameterization),我们需要对连续性的定义进行一些调整。核心思想是:我们关心的连续性(如速度、加速度)是相对于真实时间 T 的,而不是曲线的局部参数 u 的。
1. 核心变化:全局时间 (T) vs 局部参数 (u)
首先,我们要区分两个概念:
- 局部参数
u:这始终是从0到1变化的值,用来在单个贝塞尔曲线段内部进行插值。你的笔记中所有的f(u)都是基于此。 - **全局时间
T**:这是整个样条的“真实”时间轴。
假设第 i 段曲线的开始时间是 Tᵢ,结束时间是 Tᵢ₊₁。那么该段的持续时间是 ΔTᵢ = Tᵢ₊₁ - Tᵢ。
我们可以将全局时间 T 转换为该段的局部参数 u:
$u = \frac{T - T_i}{T_{i+1} - T_i} = \frac{T - T_i}{\Delta T_i}$
2. 关键:使用链式法则 (Chain Rule) 重新定义连续性
物理上的速度和加速度是曲线 P 对全局时间 T 的导数,而不是对 u 的导数。我们需要使用链式法则来连接它们:
一阶导数 (速度)
$\frac{dP}{dT} = \frac{dP}{du} \cdot \frac{du}{dT}$
从上面的公式我们知道 du/dT = 1 / ΔTᵢ。所以:
$\mathbf{P}’(T) = \frac{1}{\Delta T_i} \mathbf{P}’(u)$
这意味着,真实的速度向量是 P'(u) 的一个缩放版本,缩放因子是该段时间间隔的倒数。
二阶导数 (加速度)
对一阶导数再次求导:
$$
\frac{d^2P}{dT^2} = \frac{d}{dT}\left( \frac{1}{\Delta T_i} \frac{dP}{du} \right) = \frac{1}{\Delta T_i} \cdot \frac{d}{dT}\left(\frac{dP}{du}\right)
$$
再次使用链式法则:
$$
\mathbf{P}’’(T) = \frac{1}{\Delta T_i} \cdot \frac{d}{du}\left(\frac{dP}{du}\right) \cdot \frac{du}{dT} = \frac{1}{\Delta T_i} \cdot \mathbf{P}’’(u) \cdot \frac{1}{\Delta T_i} = \frac{1}{(\Delta T_i)^2} \mathbf{P}’’(u)
$$
真实加速度的缩放因子是时间间隔平方的倒数。
3. 如何修正上述的Splines?
现在我们把这个理论应用到样条上。
A. 贝塞尔曲线的 $C^1$ 连续性
为了实现 $C^1$ 连续,需要满足 b₄ = 2b₃ - b₂,这意味着控制点 b₃ 是 b₂ 和 b₄ 的中点(所谓的 “Mirror”)。这是因为我们假设了两段曲线的 ΔT 相同,所以我们让 P'(u) 在连接点处相等。
在非均匀时间下,我们需要让真实速度 P'(T) 相等。
- 第一段曲线(控制点 $b_0, b_1, b_2, b_3$,时长 $\Delta T_0$)在连接点 $b_3$ 的速度是:
$\mathbf{P}’(T_1) = \frac{1}{\Delta T_0} \mathbf{P}’(u=1) = \frac{3}{\Delta T_0} (b_3 - b_2)$ - 第二段曲线(控制点 $b_3, b_4, b_5, b_6$,时长 $\Delta T_1$)在连接点 $b_3$ 的速度是:
$\mathbf{P}’(T_1) = \frac{1}{\Delta T_1} \mathbf{P}’(u=0) = \frac{3}{\Delta T_1} (b_4 - b_3)$
让它们相等:
$$
\frac{3}{\Delta T_0} (b_3 - b_2) = \frac{3}{\Delta T_1} (b_4 - b_3)
$$
整理后得到:
$$
\frac{b_3 - b_2}{\Delta T_0} = \frac{b_4 - b_3}{\Delta T_1}
$$
结论:控制点 b₂, b₃, b₄ 仍然需要共线,但 b₃ 不再是中点。b₃ 到 b₂ 和 b₄ 的距离之比等于两段曲线的时间长度之比:
$$
\frac{\vert \vert b_3 - b_2 \vert \vert}{\vert \vert b_4 - b_3 \vert \vert} = \frac{\Delta T_0}{\Delta T_1}
$$
“Mirror” 关系变成了一个按时间比例缩放的“加权”关系。
均匀情况下的 Catmull-Rom
Catmull-Rom 的核心是它能自动计算每个点 Pᵢ 上的切线向量 vᵢ,计算方法是:
$\mathbf{v}i = \frac{1}{2} (\mathbf{P}{i+1} - \mathbf{P}_{i-1})$
这个公式的本质是一个几何上的平均。它假设从 Pᵢ₋₁ 到 Pᵢ 和从 Pᵢ 到 Pᵢ₊₁ 所花费的“时间”或“代价”是相同的,所以它给予了前后两个点完全相等的权重。
问题:为什么在非均匀时间下会失效?
想象一下这三个点在时间轴上的位置:
Pᵢ₋₁在T = 0Pᵢ在T = 1Pᵢ₊₁在T = 10
从 Pᵢ₋₁ 到 Pᵢ 只花了1秒,而从 Pᵢ 到 Pᵢ₊₁ 花了9秒。显然,Pᵢ 点的瞬时速度应该更接近于前一段的“高速”状态,而不是被后一段“慢速”状态平均掉。均匀公式 vᵢ = 0.5 * (Pᵢ₊₁ - Pᵢ₋₁) 完全忽略了时间信息,会导致计算出的切线不符合物理直觉。
解决方案:基于“弦速度”的加权平均
为了解决这个问题,我们需要将切线的计算从几何向量升级为物理速度。
计算弦速度 (Chord Velocity)
我们把连接相邻两个点的直线段称为“弦”。我们可以计算出每根弦的平均速度。Pᵢ前一根弦的平均速度: $\mathbf{S}{i-1} = \frac{\mathbf{P}i - \mathbf{P}{i-1}}{T_i - T{i-1}} = \frac{\mathbf{P}i - \mathbf{P}{i-1}}{\Delta T_{i-1}}$Pᵢ后一根弦的平均速度: $\mathbf{S}{i} = \frac{\mathbf{P}{i+1} - \mathbf{P}i}{T{i+1} - T_i} = \frac{\mathbf{P}_{i+1} - \mathbf{P}i}{\Delta T{i}}$
平均弦速度得到切线
最直接的非均匀 Catmull-Rom 实现,就是将这两个物理意义上的弦速度进行平均,以此作为Pᵢ点的切线:
$\mathbf{v}i = \frac{1}{2} (\mathbf{S}{i-1} + \mathbf{S}{i}) = \frac{1}{2} \left( \frac{\mathbf{P}i - \mathbf{P}{i-1}}{\Delta T{i-1}} + \frac{\mathbf{P}_{i+1} - \mathbf{P}i}{\Delta T{i}} \right)$
这个公式现在包含了时间间隔ΔT,使得时间短(速度快)的线段对切线方向和大小的贡献更大,这远比均匀版本要合理。
均匀情况下的 B-Spline
均匀 B-Spline 的节点向量是等距的,例如 [0, 1, 2, 3, 4, 5, ...]。这导致:
- 所有基函数(Basis Functions)
B(t)的形状都是完全一样的,只是在时间轴上进行了平移。 - 曲线的行为在任何地方都是一致的,控制点的移动对曲线形状的影响也是可预测且均匀的。
2. 解决方案:非均匀节点向量 (Non-Uniform Knot Vector)
非均匀 B-Spline 允许节点向量中的值不均匀分布,例如 [0, 0, 0, 1.5, 3.2, 5.0, 5.0, 5.0]。这个看似简单的改变带来了巨大的灵活性。
改变基函数的形状
B-Spline 的基函数是通过 Cox-de Boor 递归公式定义的。我们来看看这个公式(以k次样条为例):
$B_{i,k}(t) = \frac{t - t_i}{t_{i+k} - t_i} B_{i,k-1}(t) + \frac{t_{i+k+1} - t}{t_{i+k+1} - t_{i+1}} B_{i+1,k-1}(t)$
请注意分母中的tᵢ₊ₖ - tᵢ。这些项是节点向量中不同节点值之间的差。- 在均匀情况下,这些差值总是相同的。
- 在非均匀情况下,这些差值是变化的!这意味着基函数的形状本身会根据节点间距的不同而改变。如果节点靠得很近,对应的基函数会变得又高又窄;如果节点分得很开,基函数会变得又矮又宽。
控制曲线的局部行为
由于基函数的形状可以改变,我们可以通过操纵节点向量来精确控制曲线的行为:- 改变速度:将一段区域内的节点排得更紧密,会使曲线在这段“时间”内更快地变化,因为它要更快地经过受这些节点影响的控制点。
- 改变连续性:这是非均匀B-Spline最强大的特性之一。在一个节点上重复多次(增加节点的“重数”,Multiplicity),可以降低该点的连续性。对于三次B-Spline(通常是 $C^2$ 连续):
- 无重复节点 (重数为1): $C^2$ 连续 (曲率连续)。
- 重复1次 (重数为2): 降为 $C^1$ 连续 (切线连续,但曲率不连续,可形成平滑拐角)。
- 重复2次 (重数为3): 降为 $C^0$ 连续 (位置连续,但切线不连续,可形成尖角)。
- 重复3次 (重数为4,即
k+1次): 曲线会穿过对应的控制点。
总结:B-Spline 通过其核心定义——非均匀节点向量——来原生处理非均匀参数化。
总结
| 概念 | 均匀时间 (Uniform) | 非均匀时间 (Non-Uniform) |
|---|---|---|
| 核心 | 局部参数 u 的导数连续 |
全局时间 T 的导数连续 (使用链式法则) |
| $C^1$ 贝塞尔 | 控制点 b₃ 是 b₂, b₄ 的中点 |
b₂, b₃, b₄ 共线,但距离比等于时间比 |
| Catmull-Rom | 切线 vᵢ = 0.5 * (Pᵢ₊₁ - Pᵢ₋₁) |
需要使用更复杂的加权公式计算切线 |
| B-Spline | 使用等距的节点向量 | 使用非等距的节点向量,自然地处理非均匀性 |